lerail.com
15
'20
Written on Modified on
Estimation des tassements en partie haute des remblais ferroviaires sur des terrains compressibles (partie 2)
Florent Ménagé, Paula Morales-Garcia, Georges Roederer, Olivier Deck, Rasool Mehdizadeh, Stéphanie Vallerent.

ABSTRACT
Dans la première partie de cette publication, une étude paramétrique a été réalisée afin de mettre en valeur les critères influant le ratio de transmission du tassement Δ/Δ0 en fonction de différents paramètres mécaniques et géométriques des remblais et du tassement connu en partie basse des remblais Δ0 sur le logiciel Plaxis. Cependant, cette étude préliminaire (partie 1) a été réalisée avec des hypothèses dites simplificatrices de la loi de comportement du sol (linéaire élastique) et des conditions aux limites (potentiellement pénalisantes).
Cette deuxième partie de la publication vise donc à étudier l’incidence de l’utilisation d’un autre logiciel de calcul (Code_Aster) et la prise en compte d’une loi de comportement du sol de type élasto-plastique (critère de Mohr-Coulomb) sur le ratio de transmission du tassement Δ/Δ0. On vise également à quantifier la pénalisation des conditions aux limites du modèle de la partie 1 (interface considérée parfaitement glissante en pied de remblais).
Cette étude permet de confirmer l’importance de la prise en compte du ratio de transmission du tassement différentiel Δ/Δ0 dans les études de voie ferrée sur des remblais de hauteur supérieur à 2m. L’utilisation d’une loi de comportement élasto-plastique (critère de Mohr-Coulomb) permet d’optimiser le ratio de transmission. Les résultats obtenus montrent que le tassement différentiel est « moins » transmis avec une loi de comportement élasto-plastique avec les hypothèses de modélisation choisies.
Mots-clefs : #Remblais, #Tassements, #ÉlémentsFinis, #Ferroviaire, #Voie, #ConceptionJuste, #Sûreté Ferroviaire, #ComparaisonPlaxisCodeAster, #ComparaisonElastiqueElastoplastique, #RaideurSurfaciqueEquivalente
INTRODUCTION
Dans la première partie de cette publication les modèles et abaques obtenus ont été réalisés à partir d’hypothèses simplificatrices :
- L’utilisation d’une loi de comportement du sol de type linéaire élastique, qui garantit la convergence du modèle mais ne permet pas de savoir si le ratio de transmission du tassement Δ/Δ0 est pénalisé ou optimisé. Il est donc indispensable de réaliser une étude avec un sol ayant une loi de comportement élasto-plastique pour caler les limites d’utilisation d’un modèle linéaire élastique.
- L’interface parfaitement glissante en pied de remblais, particulièrement pénalisante pour les résultats et qui ne reflète pas la réalité du comportement d’un remblais.
Ainsi il convient donc là aussi de comparer les résultats avec un modèle ayant une “certaine” raideur horizontale en pied de remblais. Cette publication propose une approche pour définir la raideur horizontale équivalente d’un bloc infiniment grand. Cela permettra notamment pour la partie 3 (avec modèle 3D) de limiter le nombre de mailles et donc d’optimiser le temps de calcul.
Enfin, cette partie 2 est l’occasion de se livrer à un benchmark de logiciel : PLAXIS et Code_Aster.
1. COMPARAISON DES RESULTATS OBTENUS AVEC PLAXIS ET CODE_ASTER
1.1 Présentation de PLAXIS et Code_Aster
Le logiciel PLAXIS a été utilisé pour les calculs de la première partie de cette publication. Ce logiciel, développé par Plaxis BV (racheté par Bentley Systems), est conçu pour la modélisation et l’analyse aux éléments finis des problèmes géotechniques. Il permet notamment la génération automatique des maillages, la possibilité de choisir ou créer une loi de comportement de sol, la prise en compte des éléments de structure, de l’interaction sol-structure et la possibilité de calcul de coefficients de sécurité (TERRASOL, 2017).
Dans cette deuxième partie, le logiciel OpenSource Code_Aster, développé par EDF, est aussi utilisé pour réaliser les calculs. Code-Aster a été développé pour l’analyse structurelle et pour l’expertise et maintenance des centrales et réseaux électriques appartenant à EDF. Cet outil englobe également les analyses sur les études thermiques, les systèmes mécaniques et des ouvrages de génie civil (Durand, 2007).
1.2 Description du modèle servant à la comparaison
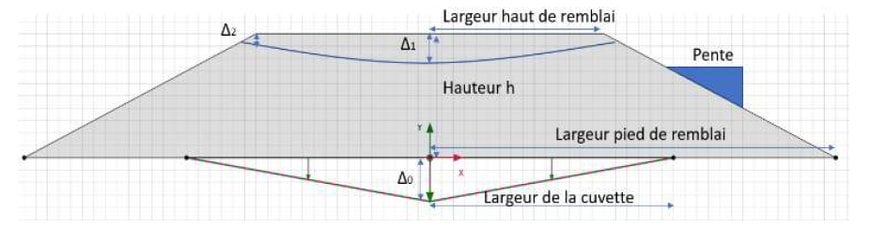
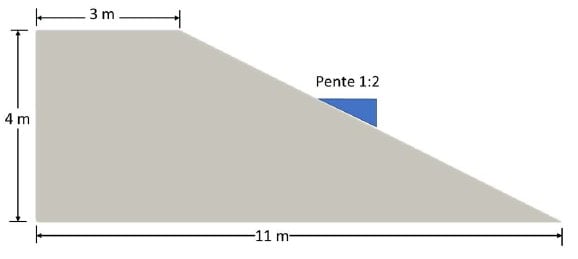
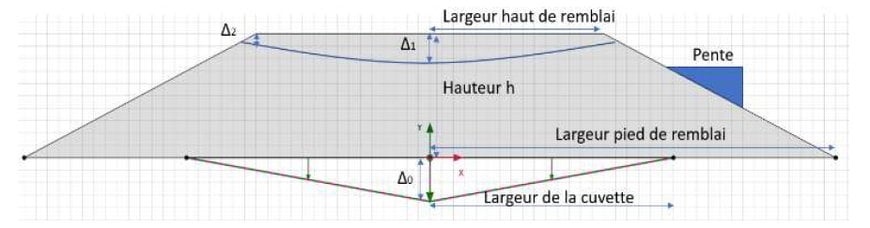
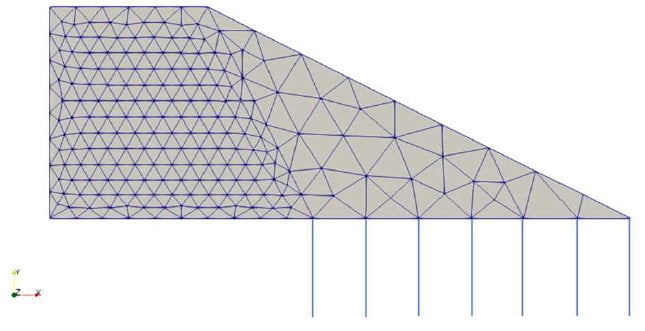
La moitié d’un remblai trapézoïdal est modélisé (Figure 1), avec comportement du sol de type linéaire-élastique, module d’Young de 30 MPa, coefficient de Poisson de 0,3, poids volumique égal à 16 kN/m3. Le déplacement imposé a été de Δ0 = 0,01 m et « L_cuvette = 5 m » (Figure 4) . Il s’agit du modèle utilisé dans la publication Partie 1.
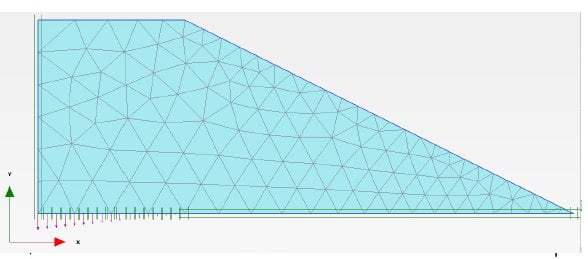
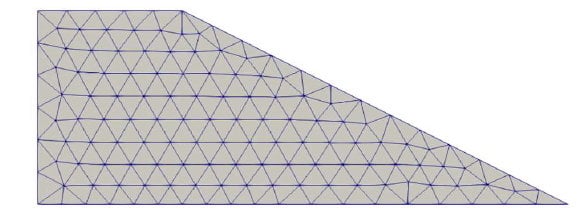
Sur PLAXIS le maillage a été réalisé automatiquement, avec une taille relative des éléments de niveau medium, qui divise le remblai en 203 éléments (Figure 2). Dans le cas de Code_Aster, le maillage a été réalisé avec une taille maximale des éléments de 0.7 m afin d’avoir un nombre de mailles et une distribution similaire du modèle sur PLAXIS (Figure 3). Les conditions aux limites sont identiques dans les deux modèles.
1.3 Résultats obtenus
La comparaison des résultats est faite à partir des ratios de transmission des tassements obtenus en haut du remblai (Δ1/Δ0 et Δ2/Δ0) et du ratio de transmission du tassement différentiel (relation entre le tassement différentiel en haut (Δ1-Δ2)/LHaut et le tassement différentiel en bas Δ0/Lcuvette).
On obtient un écart relatif de 5% pour le ratio Δ1/Δ0, de 10% pour le Δ2/Δ0 et de 4% pour la comparaison des ratios de transmission du tassement différentiel. Ces variations peuvent être notamment dues aux différences de maillage entre les deux modèles (Tableau 1).
Tableau 1:Comparaison entre les logiciels PLAXIS et Code_Aster

Un écart relatif de 5% entre 2 logiciels de calcul éléments finis est usuel. Le même ordre de grandeur avait été constaté entre CESAR et Code_Aster (RGRA, 2017).
Enfin, le ratio de transmission du tassement différentiel est 4% plus important sur Code_Aster que sur PLAXIS. On peut donc conclure que, sur ce modèle avec ce cas de charge, Code_Aster fournit des résultats plus “sécuritaires”. Dans la suite de cette étude, toutes les modélisations seront réalisées avec Code_Aster.
2. ANALYSE DE SENSIBILITE AUX CONDITIONS AUX LIMITES
Dans cette étude, le choix des conditions aux limites en pied de remblais peut modifier la manière dont le remblai se déforme face aux sollicitations imposées et donc modifier le ratio de transmission du tassement Δ/Δ0.
Dans la première partie de cette publication, la condition à la limite inférieure du remblai, en dehors de la cuvette d’affaissement, a été définie comme parfaitement glissante dans le sens de l’axe horizontal, ce qui peut être sécuritaire dans la mesure où cela augmente la probabilité d’une “instabilité de talus” (type glissement de terrain) et produit des valeurs de tassements en haut plus élevées. Afin d’évaluer l’influence de l’interface glissante en pied de remblais, le cas inverse a été étudié : les déplacements de la limite inférieure du remblai sont complètement bloqués horizontalement, en dehors de la cuvette d’affaissement. Les déplacements verticaux restent bloqués.
Les caractéristiques du modèle sont les mêmes que celles du modèle construit au chapitre 1 de cet article (cf. Figure 4). La comparaison des résultats est faite à partir des ratios de transmission des tassements obtenus en haut du remblai (Δ1/Δ0 et Δ2/Δ0) et du ratio de transmission du tassement différentiel et est présentée dans le Tableau 2.
Tableau 2: Comparaison entre les conditions aux limites horizontales libres ou bloquées avec matériau linéaire-élastique, en partie basse du remblai.

Ces résultats confirment que les tassements en haut du modèle dit “bloqué” sont inférieurs à ceux du modèle “avec interface parfaitement glissante”. Pour autant, les écarts relatifs entre ces deux modèles sont inférieurs à 1%. Ainsi les résultats ne dépendent pas de la condition à la limite inférieure du remblai tant que l'on utilise une loi de comportement linéaire-élastique pour le calcul du ratio de transmission du tassement différentiel.
3. INFLUENCE DE LA LOI DE COMPORTEMENT DU SOL
Pour les sols, on considère généralement que les effets dus à la viscosité sont négligeables et que le comportement d’un sol suit une loi élastique au début de l’application des charges jusqu’à atteindre un seuil qui marque le début d’un domaine plastique, où les déformations sont irréversibles (Dolzhenko, 2002), (Salençon, 1974).
La modélisation numérique de ce comportement élasto-plastique nécessite des modèles plus complexes qu’un modèle linéaire-élastique et implique aussi des temps de calculs et un risque de divergence plus élevés.
Afin d’analyser l’impact du choix du modèle de comportement de sol sur les résultats, le modèle réalisé pour le chapitre 1 de cette publication est repris (Figure 1) en modifiant la loi de comportement du sol en élasto-plastique. Un angle de frottement de 30°, une cohésion de 5 kPa et un angle de dilatance de 20° sont ajoutés pour le sol. Une analyse de sensibilité du maillage a conduit à raffiner légèrement celui-ci dans la zone de la cuvette d’affaissement et des tassements et .
En conservant la condition d'interface “parfaitement glissante” en pied de remblais, le modèle diverge malgré la diminution du pas de temps. La condition parfaitement glissante n’est pas réaliste et ne permet pas de prendre en compte l’interaction entre le remblai et le terrain de support. Cette instabilité du modèle a été résolue par l’ajout de “ressort” de faible raideur horizontale simulant un glissement quasi-parfait et permettant la convergence.
3.1 Ressorts de raideurs équivalentes
3.1.1 Pertinence de l’équivalence d’une modélisation à ressort
Lors de l’utilisation d’un comportement élasto-plastique sur le remblai, l’interface « parfaitement » glissante en pied de remblais augmente significativement le temps de calcul quand le modèle converge. En 2D, le temps de calcul reste faible dans l’absolu mais important relativement à un modèle où les nœuds sont collés. En prévision du modèle 3D qui comporte beaucoup plus de nœuds, il est donc indispensable de trouver une méthode permettant de s’affranchir de la modélisation d’un grand bloc nécessitant énormément de nœuds. Une modélisation avec des ressorts permet une grand économie du nombre de mailles (notamment pour le modèle 3D présenté dans la publication partie 3) mais aussi de gérer plus fidèlement l’interface remblais/sol support sous réserve de faire un modèle pour calculer les raideurs surfaciques et verticales du sol.
3.1.2 Calcul des raideurs pour un modèle à raideurs surfaciques équivalentes
Une manière pour ajouter des restrictions contrôlées pour le déplacement dans la partie inférieure du remblai, et qui permet d’obtenir des résultats assez efficacement en termes de temps de calcul, est d’utiliser un ensemble de ressorts. Ces ressorts sont situés au niveau de chaque nœud.
Comme indiqué précédemment, il est possible d’appliquer une raideur horizontale très faible pour simuler le “glissement parfait”. Cependant, cette hypothèse n’est pas réaliste et potentiellement pénalisante pour un matériau élasto-plastique. De même, une raideur très élevée est équivalente à un blocage du déplacement des nœuds qui n’est pas réaliste pour un sol de faible portance et pourrait optimiser les résultats de manière non-sécuritaire. Il faut donc calculer la raideur “surfacique” (respectivement linéique dans un problème 2D) d’un sol ayant une portance donnée pour permettre la convergence du modèle tout en ayant des résultats les plus réalistes possibles.
À cette fin, plusieurs modèles avec un bloc de sol “infiniment” grand sous le remblai ont été réalisés, en faisant varier le module d’Young du bloc (15, 30, 40, 45, 50 et 70 MPa). Ces modèles permettent de connaître la réaction des nœuds situés à l'interface du remblai avec le bloc de sol et leurs déplacements respectifs. On en déduit aisément la raideur équivalente à chaque nœud.
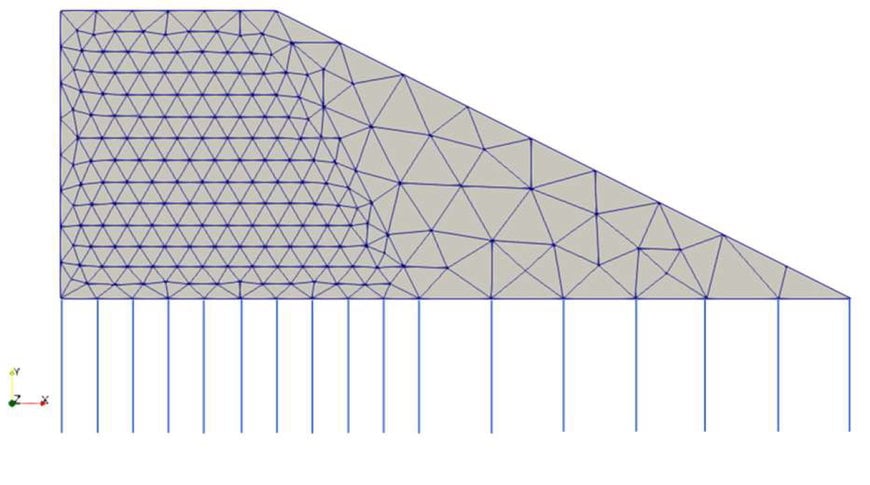
L’analyse de sensibilité de la raideur des nœuds au maillage conduit à raffiner celui-ci au niveau de la zone de contact remblai-bloc (Figure 5). La loi du comportement du bloc est définie comme linéaire-élastique, tandis que pour le remblai, la loi reste élasto-plastique. Figure 4.

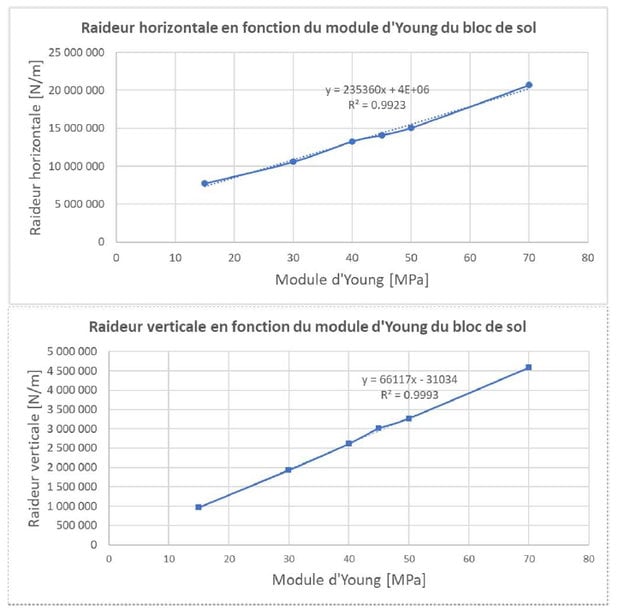
Les résultats montrent une relation linéaire entre le module d’Young du bloc (avec comportement linéaire-élastique) et les raideurs horizontales et verticales (Figure 6).
3.1.3 Comparaison des tassements en haut du remblai à bloc et du remblai à ressorts
Avec les valeurs de raideurs verticales et horizontales obtenues, un modèle à ressort est réalisé, en conservant les mêmes caractéristiques géométriques et mécaniques du modèle fait précédemment avec un comportement élasto-plastique. Le maillage est affiché dans la Figure 7.
Les résultats obtenus indiquent que les tassements du modèle à ressorts sont légèrement inférieurs à ceux obtenus avec le modèle du bloc (5% environ). En effet, les résultats d’un modèle avec 95% de la valeur des raideurs donnent des tassements très proches du modèle avec le bloc volumique infiniment grand (différences de 1%), et un modèle avec 90% de la valeur des raideurs donne des tassements légèrement supérieurs (3%) (Figure 8). Par ailleurs, il est important de souligner que le temps de calcul diminue d’environ 4 fois pour le modèle à ressorts, par rapport au modèle à bloc.
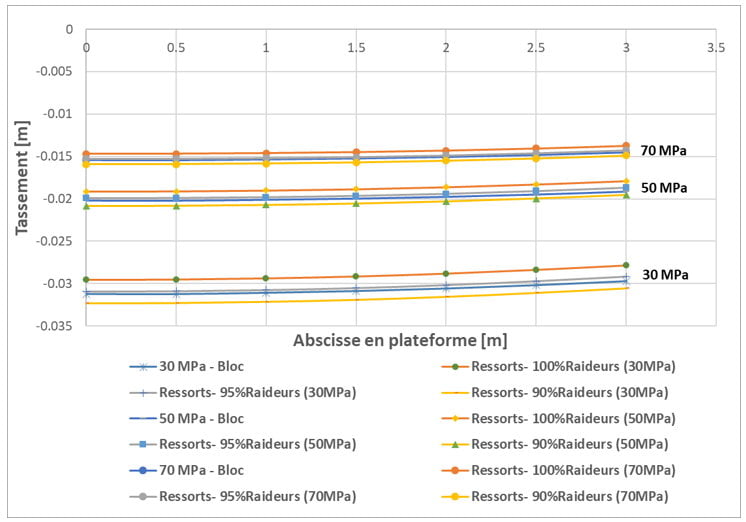
D’après ces résultats, on conclut que le modèle du remblai sur ressorts 1D (avec des raideurs entre le 90% et le 100% de celles du bloc) suffit pour représenter le comportement du sol support étant donné l’objectif de notre étude.
3.2 Remblai à ressorts en dehors de la cuvette d’affaissement
Sur la base des résultats obtenus précédemment, pour reprendre l’analyse de l’influence de la loi de comportement du sol sur le tassement obtenu en haut du remblai, un modèle avec un ensemble de ressorts en dehors de la cuvette d’affaissement est considéré, avec des raideurs horizontales telles que calculées dans le chapitre 3.1, et des raideurs verticales égales à 3x104 GN/m, afin de simuler la condition de déplacement bloqué verticalement sur une partie du modèle initial (Figure 9). Ce blocage des déplacements verticaux sous une partie du remblai est indispensable pour générer un « tassement différentiel ».
Pour mesurer la sensibilité de la raideur horizontale en pied de remblais, nous avons commencé par faire varier la raideur horizontale parmi une gamme de valeurs équivalente à un sol parfaitement glissant (10, 100, 1000, 10000 N/m).
Dans ce cas, les modèles convergent mais les résultats montrent un comportement inattendu, car le tassement Δ2 est supérieur au tassement Δ1. On constate en effet sur la Figure 10 que les isovaleurs du déplacement vertical suivent, entre les abscisses 4m et 8m environ, un comportement qui peut indiquer qu’une partie du remblai est plastifiée et subit des déformations importantes par rapport aux valeurs obtenues avec le modèle linéaire-élastique.
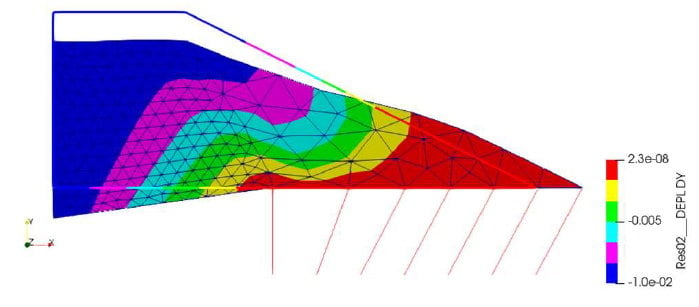
Ces premiers résultats expliquent ainsi la divergence du modèle en cas de raideur horizontale nulle où le remblai « coulerait » sur le sol.
Ainsi, deux modèles sont évalués pour déterminer si la variation de la raideur horizontale influence le taux de transmission ou si les résultats de ces modèles peuvent être comparés aux résultats obtenus avec le modèle glissant de la Partie 1. À cette fin, un modèle qui évalue un cas extrême des conditions de glissement presque complètement bloquées dans le sens horizontal est d’abord réalisé (raideur très élevée 1X1012 N/m). Les résultats sont montrés dans Tableau 3 modèle 1, Figure 11.
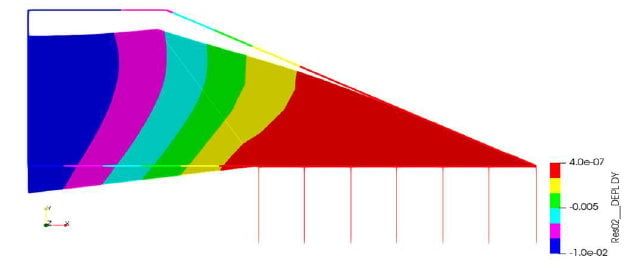
Ensuite, le modèle est évalué avec des valeurs de raideur transversale conformes aux raideurs équivalentes présentées sur la Figure 6 (c’est-à-dire 10 MN/m pour le cas d’un remblai sur un sol de portance 30MPa), ce qui représente une valeur plus proche d’un cas réel. Les résultats de ce modèle sont présentés dans la Figure 12 et le Tableau 3 modèle 2.
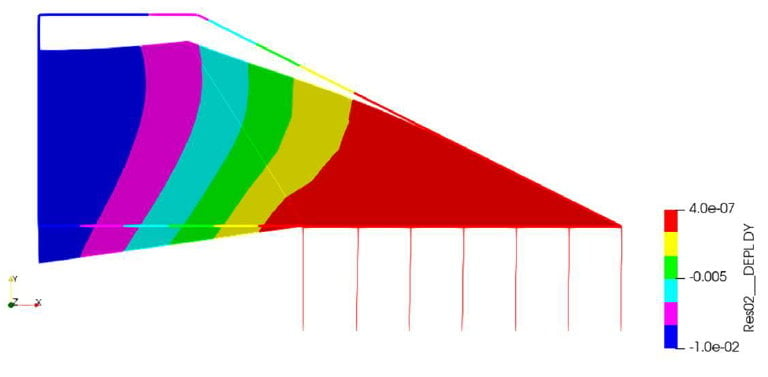
Étant donné que la variation de la raideur horizontale des ressorts ne varie pas significativement les résultats, on peut conclure que lorsque le modèle élasto-plastique « ne coule pas » sur le sol, les tassements obtenus en haut du remblai sont proches.
Les résultats obtenus sont alors comparés au modèle linéaire-élastique avec des conditions parfaitement glissantes (Tableau 3 modèle 3). Ces résultats indiquent que la loi de comportement du sol peut faire varier significativement les résultats obtenus pour le tassement différentiel en haut. Il faut cependant souligner que les résultats du modèle linéaire-élastique sont plus pénalisants que ceux du modèle élasto-plastique. Il est donc remarquable qu’une modélisation linéaire élastique peut être utilisé en première approche car la convergence est beaucoup plus rapide et aisée à obtenir tout en restant sécuritaire dans le respect des valeurs et hypothèses prises pour cette étude de sensibilité.
Tableau 3. Comparaison entre les modèles linéaire-élastique et élasto-plastique avec différentes conditions aux limites

4. ANALYSE DE SENSIBILITE
4.1 Sensibilité sur la hauteur du remblai
Maintenant que l’incidence sur les résultats du logiciel de calcul, des conditions aux limites et de la loi de comportement du sol a été évalué, nous allons faire une analyse de sensibilité du ratio de transmission du tassement différentiel lorsque la hauteur du remblai est variée.
Pour ce faire, trois modèles sont testés, avec des hauteurs de 2m, 4m et 7m. La pente des remblais est conservée à ½, les caractéristiques mécaniques sont les mêmes que celles du remblai étudié dans le chapitre 3 de cette publication et les deux lois de comportement du sol traités précédemment sont évaluées, ce qui implique la réalisation de remblais à ressorts. Pour les ressorts, la raideur horizontale est égale à 10 MN/m (équivalent à un bloc sous le remblai de portance 30 MPa) et la raideur verticale égale à 10x1012 N/m. Le déplacement imposé est Δ0 = 0,01 m et « L_cuvette = 5 m ».
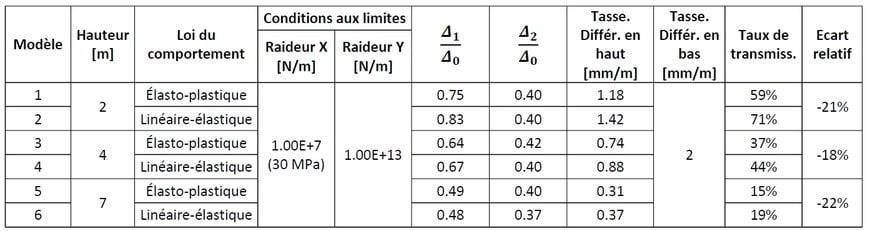
Les résultats sont présentés dans le Tableau 4, et permettent de conclure que, comme dans le cas linéaire-élastique sans ressorts (Partie I de cette publication), le ratio de transmission augmente à mesure que la hauteur du remblai diminue, ce qui se trouve cohérent car les remblais plus hauts peuvent plus facilement dissiper, dans toute leur épaisseur, le déplacement imposé en bas. Cependant, il faut souligner que, dans la réalité, les remblais plus épais vont générer plus de surcharges sur le sol support, ce qui peut signifier des déplacements en pied de remblai plus importants que pour un remblai plus petit. Il faut donc être vigilent sur le taux de transmission du remblai. Un tassement différentiel important sur un remblai de grande hauteur est potentiellement aussi préjudiciable sur une voie ferrée qu’un tassement différentiel plus faible sur un remblai de faible hauteur.
D’autre part, la comparaison entre les cas linéaire-élastique et élasto-plastique confirme que le cas linéaire-élastique donne des résultats avec des ratios de transmission du tassement différentiel plus élevés, l’écart relatif entre les résultats étant d’environ 20%.
Tableau 4. Modèles réalisés pour tester la sensibilité des résultats face à la variation de la hauteur du remblai
4.2 Sensibilité sur la raideur du sol support
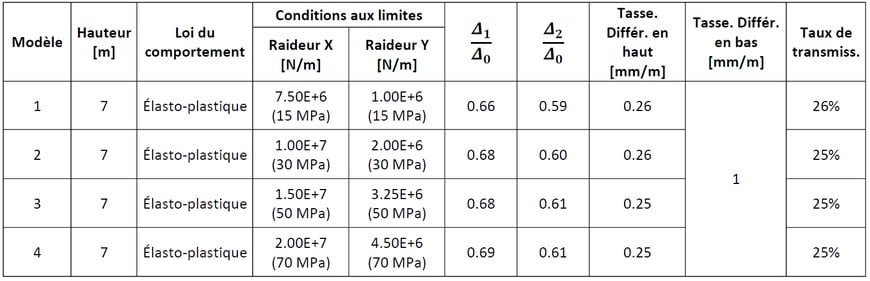
Dans le but d’évaluer l’influence que la raideur du sol support du remblai peut avoir sur les résultats, une analyse de sensibilité est faite pour un remblai de 7 m de hauteur, avec un déplacement imposé de Δ0 = 0,01 m et « L_cuvette = 10 m ». Ce remblai, qui a une loi du comportement élasto-plastique, est modélisé comme un remblai à ressorts en dehors de la cuvette d’affaissement, et les raideurs horizontales et verticales sont variées d’après les valeurs obtenues dans la Figure 6 pour les blocs de portance égale à 15, 30, 50 et 70 MPa.
Les résultats, présentés dans le Tableau 5, montrent que la prise en compte de l’existence d’un bloc du sol sous le remblai, avec une raideur donnée, a une influence négligeable sur les résultats, car le ratio de transmission est toujours obtenu d’environ 25% et la différence entre le cas avec la raideur la plus faible et celui avec la raideur la plus élevée, donne des écarts inférieurs à 1%.
Tableau 5. Modèles réalisés pour tester la sensibilité des résultats face à la variation de la raideur du sol support
4.3 Sensibilité sur la largeur de la cuvette
Afin d’évaluer l’impact que la largeur de la cuvette imposée en partie basse du remblai peut avoir sur le taux de transmission du tassement différentiel, une analyse est faite pour un remblai de 4m de hauteur, avec une loi du comportement élasto-plastique et des ressorts équivalents à un sol support de 30 MPa de module. La cuvette est évaluée pour des largeurs 1m, 3m, 5m, 7m et 9m, afin de pouvoir comparer également ces résultats avec ceux obtenus dans la Partie I de cette publication et qui ont été représentés sous forme d’abaque (Figure 4, Partie I). Le déplacement imposé est égal à 0.01 m.
D’après les résultats obtenus (Error! Reference source not found.), il s’ensuit d’abord que la largeur de la cuvette en bas du remblai impacte le tassement différentiel en haut, et son impact n’est pas proportionnel à la taille de la cuvette imposée. Ainsi, on observe une augmentation du tassement différentiel en haut jusqu’à une cuvette d’environ 3 m de large, puis une diminution progressive. Malgré cela, le taux de transmission (relation entre le tassement différentiel en haut et en bas) augmente à mesure que la taille de la cuvette imposée augmente.
D’un autre côté, la comparaison entre les résultats obtenus ici (remblai à ressorts, élasto-plastique, sur Code-Aster), et ceux obtenus dans la Partie I (remblai bloqué en partie inférieure, linéaire-élastique, sur PLAXIS), permet de conclure que la différence entre les taux de transmission est de 10% maximum. Cette comparaison est assez importante car elle permet de connaitre la superposition des écarts dus aux hypothèses simplificatrices des modèles réalisés dans la Partie I.
5. CONCLUSION
Les analyses de sensibilité menées dans cette étude montrent que l’impact des conditions aux limites dans les cas linéaire-élastiques et du logiciel choisi est faible (écarts relatifs inférieurs à 5% sur les résultats), ce qui permet de choisir les conditions aux limites et le logiciel qui offre le temps de calcul le plus faible.
A contrario, les analyses de sensibilité montrent que le choix de la loi de comportement du sol a un effet important avec des écarts relatifs du ratio de transmission de 15% à 20% sur les géométries testées. Ces écarts sont significatifs et incitent donc à la vigilance sur le choix du comportement de sol :
- Un comportement de sol élastique linéaire avec sol parfaitement glissant permet d’avoir un résultat très rapidement mais plus pénalisant (taux de transmission du tassement plus élevé que dans la réalité)
- Un comportement de sol élasto-plastique est plus complexe à calibrer et à faire converger mais procure des résultats optimisés en terme de mesures du taux de transmission du tassement différentiel.
Par conséquent, compte tenu de la complexité pour avoir la convergence du modèle élasto-plastique, des faibles différences entre les résultats des modèles sous la variation des autres paramètres, et, en outre, du fait que les tassements différentiels en haut du remblai pour les modèles linéaires-élastiques ont toujours été supérieurs, on conclut que les tassements différentiels en pied de remblais et en haut du remblai diffèrent largement et nécessitent une analyse au cas par cas.
Il est pertinent, en fonction de la phase du projet, de se contenter d’un modèle linéaire élastique (phase amont) ou au contraire d’utiliser un modèle plus précis avec une loi de comportement élasto-plastique permettant une optimisation intéressante de l’ouvrage voie ferrée situé en haut du remblai.
On retiendra en particulier que le tassement différentiel en haut d’un remblai de 7m est potentiellement 5 fois plus faible que le tassement différentiel au niveau de la sous-couche.
RÉFÉRENCES
Alamaa, A. (2016). High-speed railway embankments— a comparison of different regulations. Stockholm: KTH Royal Institute of Technology .
Bentley Systems. (2019). Reference Manual Plaxis. Edition V20.
Boutonnier, L., Hajouai, F., Bacar Fadhuli , N., & Gandille, D. (2013). LGV EST lot 41 : Tassements calculés puis mesurés sous remblais. Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering. Paris.
Carter, J., Desai, C., Potts, D., Schweiger , H., & Sloan, S. (2000). COMPUTING AND COMPUTER MODELLING IN GEOTECHNICAL ENGINEERING, pp. 1157-1252.
Dolzhenko, N. (2002). THESE : ETUDE EXPERIMENTALE ET NUMERIQUE DE MODELE REDUIT BIDIMENSIONNEL DU CREUSEMENT D’UN TUNNEL. DEVELOPPEMENT D’UNE LOI DE COMPORTEMENT SPECIFIQUE. Lyon: DEA Génie Civil - INSA Lyon.
Durand, C. (2007). FREE SOFTWARE FOR COMPUTATIONAL MECHANICS: EDF’S CHOICE.
Forest, S., & Amestoy, M. (2015). MECANIQUE DES MILIEUX CONTINUS. Paris: ECOLE DES MINES DE PARIS.
Grémer, J., & Gaudeul, A. (2004). Quelques éléments d'économie du logiciel libre. Réseaux, 111-139.
GTR . (2000). Réalisation des remblais et des couches de forme. Bagneux: Laboratoire Central des Ponts et Chaussées.
INPL Nancy . (s.d.). Propriétés Mécaniques et Physiques des Sols. Retrieved from http://tice.inpl-nancy.fr/modules/sciences_techniques/Proprietes-Meca-Sols/general/index.html
Larsson, R., Bengtsson, P.-E., & Eriksson, L. (1997). Prediction of settlements of embankments on soft, fine-grained soils. LINKÖPING: SWEDISH GEOTECHNICAL INSTITUTE.
Nguyen, T. T., & Trinh, T. H. (2012). ELEMENTS FINIS : DU CLASSIQUE AU ISOGEOMETRIQUE. Nice: UNIVERSITÉ DE NICE - SOPHIA ANTIPOLIS.
Potts, D. M., & Zdravkovic, L. (1999). Finite element analysis in geotechnical engineering. London: Thomas Telford Publishing.
Qin , Y., Zhang, J., Zheng, B., & Ma, X. (2009). Experimental study for the compressible behavior of warm and ice-rich frozen soil under the embankment of Qinghai–Tibet Railroad. Cold Regions Science and Technology, 148-153.
Quezada, J. C. (2014). Mécanismes de tassement du ballast et sa variabilité. Montpellier : Université Montpellier 2.
RFR & SNCF. (2006, Avril 30). IN3279 - Référentiel technique pour la réalisation des LGV - Partie Equipements Ferroviaires. Retrieved from https://victimestgvaccident.files.wordpress.com/2016/12/in3279.pdf
RGRA. (2017). Révue générale des routes et de l'aménagement . Éditeur de référence des infrastructures pour la mobilité.
Said-Alami, S., Reiffsteck, P., & Cuira, F. (2017). Méthode d’estimation des tassements des sols fins sous les remblais d’infrastructures ferroviaires pour lignes à grande vitesse. Revue Française de Géotechnique, 153,3.
Salençon, J. (1974). Théorie de la plasticité pour les applications à la mécanique des sols. Paris: Éditions Eyrolles.
SimScale. (2020, 06 28th). What Are Boundary Conditions? Retrieved from https://www.simscale.com/docs/simwiki/numerics-background/what-are-boundary-conditions/
Techniques de l'ingénieur. (s.d.). Terrassement et géomembranes. Techniques de l'ingénieur.
TERRASOL. (2017). Logiciel éléments finis 2D dédié à la géotechnique. Retrieved from Terrasol-Setec: https://www.terrasol.fr/catalogue/plaxis-2d
Terrassiers de France. (2009). Guide pour la réalisation des terrassements des plateformes de bâtiments et d’aires industrielles dans le cas de sols sensibles à l’eau. Paris: Syndicat Professionnel des Terrassiers de France.
Yang, Y., Liu, S., Deng, Y., & Jing , F. (2008). Differential settlement controlling criteria of highway transition sections on soft soil foundation). Dongnan Daxue Xuebao (Ziran Kexue Ban)/Journal of Southeast University (Natural Science Edition).

