lerail.com
14
'20
Written on Modified on
Estimation des tassements en partie haute des remblais ferroviaires sur des terrains compressibles (partie I)
Florent Ménagé, Paula Morales-Garcia, Amaury Bouffard, Guilherme Cunha de Barros Santos, Georges Roederer, Olivier Deck, Rasool, Mehdizadeh, Stéphanie Vallerent

ABSTRACT
La construction de lignes à grande vitesse implique la réalisation de remblais reposant sur des terrains de nature différente. Lorsque ces remblais sont construits sur des sols compressibles, les charges induites par leur poids propre et celui des trains, engendrent des tassements liés à la consolidation des terrains supports. Ce phénomène génère à la fois des tassements en partie basse des remblais (Δ0) qui se transmettent à la plateforme en partie supérieure (Δ) et qui peuvent dépasser des valeurs acceptables pour la pérennité des voies ferrées sans ballast en particulier, avec des conséquences directes sur la sécurité des voyageurs. L’objectif de cette étude est d’évaluer le taux de transmission du tassement Δ/Δ0 en fonction de différents paramètres mécaniques et géométriques des remblais et du tassement Δ0, afin de construire ainsi des abaques permettant de déterminer le ratio de transmission d’une manière pratique. Cet article vise aussi à mettre en avant les risques d’incompréhension entre l’ingénieur voie qui définit le tassement maximal admissible (Δ) et l’ingénieur géotechnicien qui calcule le tassement du terrain support du remblai (Δ0).
Mots-clefs : #Remblais, #Tassements, #Éléments Finis, #Ferroviaire, #Voie, #Conception Juste, #Sûreté Ferroviaire
INTRODUCTION
La problématique des remblais des lignes à grande vitesse construits sur des terrains compressibles a été abordée par de nombreux chercheurs pour comprendre comment le sol support des remblais peut subir un tassement associé aux charges qui lui sont imposées (Qin , Zhang, Zheng, & Ma, 2009), (Boutonnier, Hajouai, Bacar Fadhuli , & Gandille, 2013). Si Δ0 représente l’amplitude maximal de ce tassement, il ne peut pas être considéré uniforme sous l’emprise surfacique du remblai et s’accompagne donc d’un tassement différentiel de la base du remblai. Ce tassement différentiel sera à l’origine d’un tassement Δ en partie haute du remblai, également non uniforme. Les voies ferroviaires, sensibles aux tassements, notamment les tassements différentiels, elles exigent une bonne prédiction du processus de consolidation des terrains support des remblais et des phénomènes de transmission de ces tassements vers la surface, afin de déterminer le type de remblai et les éventuels renforcements à prendre en compte pour l’ouvrage (Alamaa, 2016)
La recherche des études réalisées sur le domaine permet de trouver des travaux comme ceux réalisés par Said-Alami, Reiffsteck & Cuira (2017) et Larsson, Bengtsson & Eriksson (1997) qui proposent des méthodes analytiques pour l’estimation des tassements des sols fins sous les remblais ferroviaires, ou celui réalisé par Yang, Liu, Deng & Jing (2008) qui analyse la relation entre le tassement différentiel du sol support et la hauteur et module d’Young du remblai. Mais aucune méthode opérationnelle n’est trouvée pour déterminer comment le tassement généré sur le sol support du remblai est transmis au travers de celui-ci et quel tassement est obtenu au niveau de la plateforme comme conséquence de cet affaissement en partie basse.
L’objectif du présent article est de proposer un modèle reliant le tassement en bas du remblai (Δ0), donné par les géotechniciens, avec celui en partie supérieure du remblai (Δ), requis par les ingénieurs de la voie ferrée. A partir d’une modélisation numérique par éléments finis sur PLAXIS 2D, une analyse paramétrique a été réalisée en faisant varier la hauteur, les paramètres mécaniques du remblai (Module d’Young) et la largeur du tassement en pied de remblai. Les résultats obtenus seront présentés sous forme d’abaques qui permettent d’estimer l’ordre de grandeur du tassement différentiel en haut du remblai selon les caractéristiques propres de chaque cas. Enfin, des exemples d’applications sont présentés.
1. LA PROBLÉMATIQUE DES TASSEMENTS EN REMBLAIS FERROVIAIRES
Un remblai ferroviaire est une surélévation d’une voie ferroviaire sur le terrain. Les matériaux qui le composent dépendent de terrain du support, de la disponibilité de matériaux, des efforts et conditions de travail auxquels le remblai sera soumis... Sa géométrie varie également selon les conditions particulières à chaque cas.
Le terrain support d’un remblai subit un tassement, associé à des déformations verticales dues à l’application du chargement vertical associé au poids du remblai en particulier. On distingue traditionnellement trois types de tassements : tassement instantané associé à la déformation élastique des matériaux, tassement de consolidation associé à l’expulsion des surpressions interstitielles et le report des charges sur le squelette granulaire et tassement associé au fluage ou à la réorganisation du squelette granulaire (Quezada, 2014). Ces tassements ne peuvent pas être uniformes car le chargement vertical associé au poids du remblai ne l’est pas compte tenu de sa forme trapézoïdale.
Contrairement au tassement instantané qui peut être immédiatement compensé par le nivellement du remblai lors de sa construction, le tassement de consolidation est différé dans le temps et impacte directement la sécurité de l’infrastructure.
Par conséquent, lorsque les remblais ferroviaires sont réalisés sur des sols compressibles comme les plaines ou vallées alluvionnaires, ce terrain support est susceptible de faire l’objet d’un tassement lié à l’expulsion d’eau et à l’élimination de la surpression interstitielle. Celui-ci engendre progressivement un tassement en partie basse des remblais (Δ0) qui se transmet à la partie haute (Δ). Ces affaissements, lorsqu’ils sont de nature « différentielle », sortent parfois des gammes de valeurs acceptables pour les voies ferrées sans ballast notamment, avec des conséquences sur la sécurité des voyageurs (risque de déraillement).
Ainsi, connaître le tassement du remblai en haut est crucial pour le dimensionnement de la voie ferrée. L’analyse géotechnique se focalise sur le tassement du sol support, c’est-à-dire, le tassement en pied de remblais, et le désigne par abus de langage par « tassement ». Dans les projets récents de dimensionnement de voie ferrée, le tassement différentiel induit en haut du remblai est rarement calculé et l’hypothèse est prise que le tassement différentiel en pied du remblai est identique au tassement en haut du remblai. Cette hypothèse conservatrice est-elle justifiée ? Un tassement du sol support de 1cm engendre-t-il un tassement de la couche sous voie ferrée de 1cm (à l’aplomb du tassement du sol support de 1cm) ? Y a-t-il une atténuation ? La forme du tassement en pied de remblai est-elle la même que le tassement en haut du remblai ? Ces questions sont abordées dans nos travaux.
2. MÉTHODOLOGIE
Compte tenu de la répétitivité de la forme du remblai une analyse par éléments finis en 2D avec PLAXIS a été retenue en première approche. La rapidité de ce type de calcul est aussi un avantage pour réaliser une étude de sensibilité. Par ailleurs, ce type de modèles utilise l’hypothèse des déformations planes, ce qui est acceptable pour les modèles représentant une section transversale du remblai, car ils visent à évaluer l’influence de la largeur de la cuvette d’affaissement dans la direction transversale du remblai.
La méthode suivie est la suivante : définition des scénarios, paramètres et hypothèses de modélisation, post-traitement des résultats pour extraire les valeurs nécessaires à la construction des abaques de synthèse puis validation des résultats en les confrontant à des modélisations numériques en 3D et un modèle physique.
3. MODÉLISATIONS NUMÉRIQUES EN 2D
En première approche, des modèles 2D transversaux, ont été utilisés pour les calculs. La simplicité du modèle permet aussi d’obtenir des résultats rapidement afin de réaliser une étude de sensibilité. Les modélisations utilisent l’hypothèse des déformations planes, ce qui implique que le remblai et le tassement modélisés ont une extension infinie. On ne tient donc pas compte de l’influence de la variabilité géométrique du remblai ou du tassement dans la direction longitudinale. Le logiciel qui a été choisi pour les calculs est PLAXIS2D.
3.1 Hypothèses
- Géométrie du remblai :
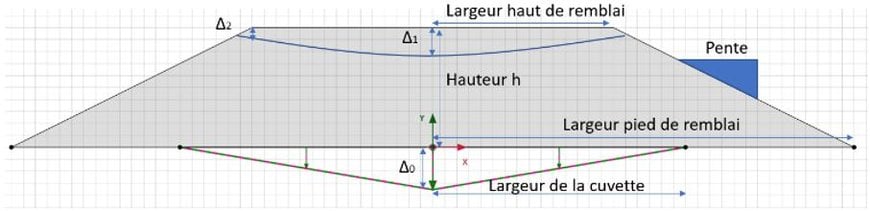
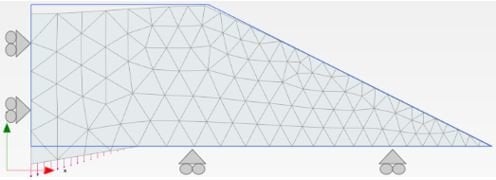
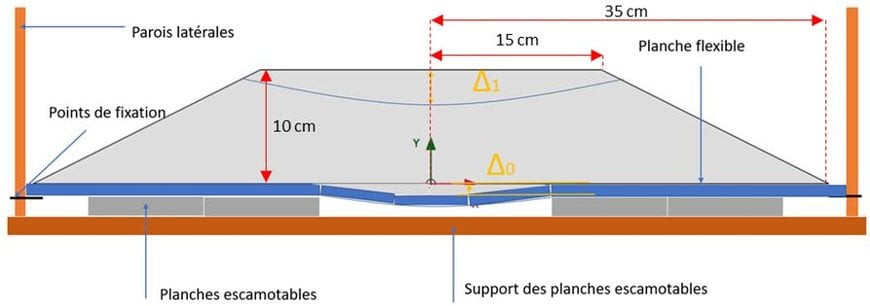
La géométrie du remblai est présentée en Figure 1. La cuvette représente le tassement en pied du remblai, caractérisée par la largeur « L_cuvette » et le tassement maximal Δ0. Le tassement en haut est représenté par Δ1 au milieu de la plateforme et Δ2 à l’extrémité de celle-ci.
Pour simplifier le modèle, la largeur de la plateforme et la pente du remblai sont fixées à partir des valeurs standards ou typiques. La largeur de la plateforme est fixée à 6 m, et la pente du remblai à 1:2. Trois hauteurs de remblai sont considérées: 1m, 4m et 7m.
- Propriétés géomécaniques :
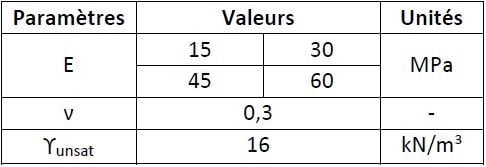
Un modèle linéaire-élastique représente le comportement du sol. Les hypothèses choisies sont de travailler avec des matériaux qui correspondent aux valeurs suivantes, où E représente le module d’Young, ν représente le coefficient de Poisson et ϒunsat représente le poids volumique du terrain :
Tableau 1. Valeurs géomécaniques utilisées
- Déplacement imposé :
Le phénomène de consolidation n’est pas modélisé explicitement. Un déplacement sur la frontière inférieure du modèle est imposé directement afin de reproduire ce tassement. Le déplacement est considéré centré et symétrique, car il est la conséquence du poids propre du remblai, lui-même centré et symétrique.
À partir des modèles réalisés (Tableau 4), on observe que l’amplitude des déplacements en haut de remblai Δ varie linéairement avec celle du déplacement en pied de remblai Δ0. Cela est cohérent avec la modélisation élastique linéaire en l’absence de loi de contact. On en conclu que les abaques peuvent être produits indépendamment de la valeur de l’amplitude maximale Δ0 en normalisant le déplacement maximal Δ/Δ0, sous réserve de valider l’utilisation d’une loi élastique linéaire. Par conséquent, pour les modèles utilisés pour la création des abaques, une valeur maximale de déplacement vertical Δ0= 1 cm au milieu du remblai a été prise. La largeur d’une demi-cuvette « L_cuvette » varie également entre 1 m et la largeur totale du remblai « L_remblai ».
Voir Figure 1. Représentation de la géométrie du remblai.
Quant à la forme de la cuvette, une comparaison entre différentes formes a été effectuée afin de comprendre l’impact de celle-ci sur les résultats. Pour ce faire, plusieurs modèles ont été réalisés, tout en gardant le même déplacement au centre du remblai, la même largeur de cuvette et le même volume déplacé. Étant donné que la cuvette a été découpée en 3 morceaux linéaires, il a été nécessaire de respecter l’équation suivante pour obtenir le même volume déplacé : ∆_0=h=h_1=h_2+h_3 (Figure 2).
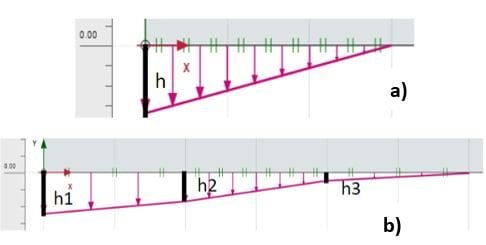
Les comparaisons ont été donc faites entre les tassements obtenus en surface ∆_(1_ Lin) pour le cas de la cuvette linéaire (Figure 2a) et ∆_(1_Frac) pour la cuvette par morceaux (Figure 2b), dont les résultats montrent que la forme de la cuvette a une influence négligeable (inférieur à 5%) sur le déplacement en haut si on conserve le même volume de déplacement (Tableau 2).
Tableau 2. Modèles élaborés pour la comparaison de la forme de la cuvette
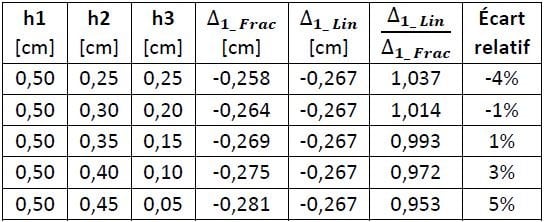
Par conséquent, dans le but de simplifier le modèle, un déplacement linéaire a été considéré.
La géométrie et le déplacement imposé étant considérés symétriques, seule la moitié droite du remblai a été modélisée.
- Maillage :
Une étude de sensibilité à la taille du maillage a été réalisée avec 7 modèles, en faisant varier le paramètre représentatif du maillage sur PLAXIS, qui est la multiplication de la taille relative des éléments r_e et la constante 0,06. La valeur de r_e est comprise entre 5 niveaux globales :
Tableau 3. Valeurs prédéfinies de la taille relative des éléments r_e (Bentley Systems, 2019)
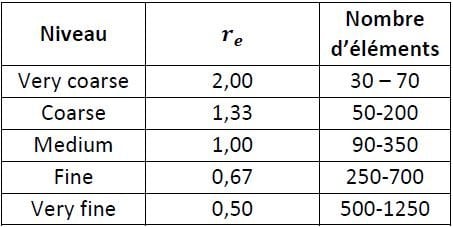
Le paramètre a été donc varié entre 0,4 et 0,005. Avec cela, l’écart obtenu entre le déplacement maximal en haut du remblai est compris entre 0,02% et 0,2%, ce qui est relativement faible et montre donc que le maillage peut être relativement grossier sans avoir beaucoup d’influence sur les résultats. Par conséquent, un paramètre intermédiaire, égal à 0,06, a été pris.
- Conditions aux limites :
En raison de la symétrie du remblai et du choix de ne modéliser que la moitié droite, le déplacement vertical à l’extrémité gauche est libre et le déplacement horizontal bloqué.
Pour la limite inférieure du remblai, le déplacement horizontal est libre mais le vertical est bloqué dehors la cuvette d’affaissement et fixé à l’intérieur de celle-ci avec les valeurs de déplacement imposées. Cette situation ne représente pas la réalité car il y en existe une couche de terrain sur laquelle repose le remblai, qui ne permet pas que le mouvement horizontal de cette extrémité soit complétement libre. Néanmoins, afin de maximiser les déplacements verticaux en haut du remblai, cette limite a été prise comme parfaitement glissante (Figure 3).
3.2 Modèles transversaux
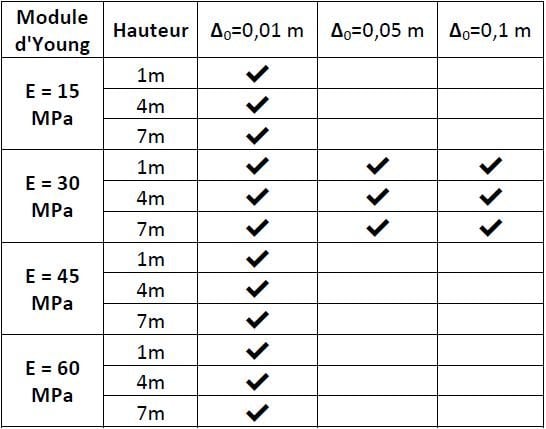
Au total 18 modèles ont été réalisés et sont présentées dans le Tableau 4. La multiplicité des tests a été fait avec l’interpréteur de PLAXIS et l’aide de scripts Python. Ce grand nombre de tests permet d’avoir une meilleure idée de ce qui se passe dans un certain nombre de cas.
Tableau 4. Modèles 2D (transversaux) élaborés
3.3 Résultats
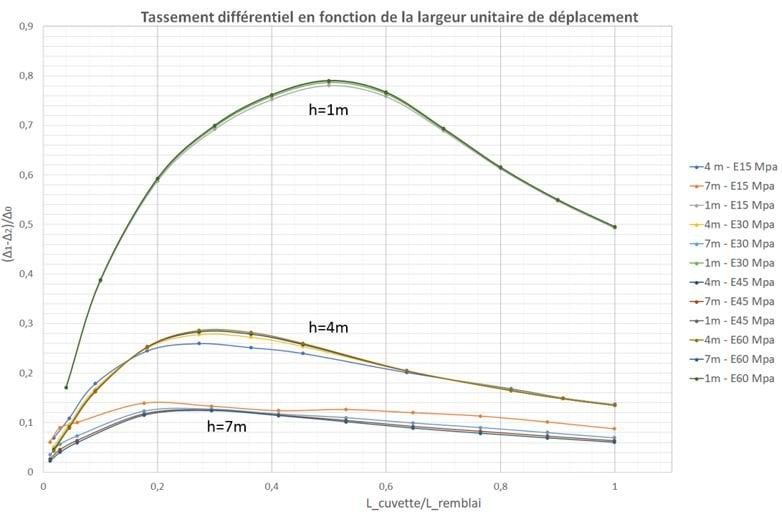
Les résultats sont représentés sous la forme d’abaques (Figure 4). Les courbes représentent le taux de transmission (le tassement différentiel en haut de remblais ∆1-∆2 sur le déplacement en pied de remblai ∆0) en fonction du ratio L_cuvette/L_remblai. Ces deux ratios sont compris entre 0 et 1.
Trois groupes de courbes sont observés. Elles sont toutes croissantes linéaires dans une première portion puis atteignent un maximum avant de décroitre. Cette particularité peut s’expliquer grâce à la différence ∆1-∆2. En effet, lorsque le ratio L_cuvette/L_remblai croit, ∆1 puis ∆2 croissent également. Dans un premier temps, le milieu du remblai est impacté puisque le déplacement se trouve juste dessous. Petit à petit, la largeur de la cuvette augmentant, le bord de droite commence à être impacté, alors ∆2 augmente. La différence ∆1-∆2 devient globalement constante, ce qui crée une décroissance du ratio (Δ1 - Δ2)/Δ0 et donc un maximum.
Les courbes sont groupées en fonction de la hauteur des remblais. Lorsque la hauteur est faible, le taux de transmission est élevé, proche de 1. En effet un remblai qui ferait par exemple 10 cm de haut, auquel on attribue un déplacement de 10 cm en pied, sera bien déplacé en haut d’une valeur proche de 10 cm. Ainsi, pour des remblais de faible hauteur, on peut s’attendre à un taux de transmission élevé, c’est-à-dire quasiment aucune atténuation du tassement par le remblai. Il faut toutefois noter que pour ces mêmes remblais, le poids sera faible et l’amplitude attendue du tassement Δ0 également faible, ce qui conduira à un tassement différentiel absolu en partie supérieure faible également.
Il est observé également que le module de Young n’a aucune influence significative. Ce résultat est attendu compte tenu des choix de modélisation (comportement linéaire-élastique). Les fluctuations observées rendent probablement compte d’incertitudes liées aux algorithmes de résolution par éléments finis.
On remarque enfin que le maximum de tassement différentiel est atteint d’autant plus rapidement que la hauteur du remblai est élevée. Pour un remblai de 1m, le maximum est atteint pour L_cuvette/L_remblai= 0,5 alors que pour un remblai de 7m, le maximum est atteint pour L_cuvette/L_remblai= 0,22.
Dans le cadre de la recherche pour expliquer le pic de la Figure 4, il est tout d’abord cohérent que, pour un remblai plus épais, l’influence d’un déplacement se répercute plus rapidement entre le haut du remblai au centre et le haut du remblai à droit. On constate donc qu’une tendance qui pourrait expliquer ce phénomène est la transmission de la répercussion sous une forme circulaire.
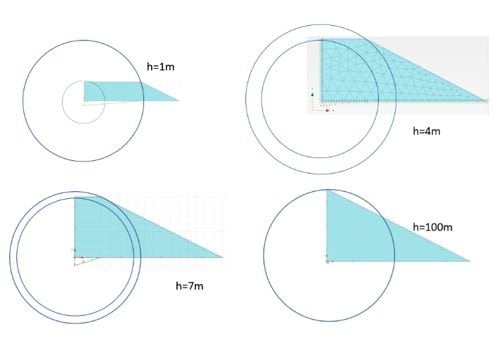
Pour chaque cas, un cercle a été tracé et coupe le centre haut du remblai (au point où on relève ∆2). Plus la hauteur du remblai est importante, plus les cercles sont rapprochés. Leur proximité tendrait éventuellement à ce que le maximum sur l’abaque se rapproche de 0. Il y a donc une certaine logique que le maximum se rapproche de 0 lorsque l’épaisseur du remblai augmente.
4. VALIDATIONS DES RÉSULTATS
Les résultats de la modélisation 2D ont été comparés à une modélisation numérique 3D réalisée avec le logiciel PLAXIS 3D d’une part et à un modèle physique réduit d’autre part.
4.1 Modèle 3D
Un modèle 3D de même géométrie et mêmes propriétés mécaniques que le modèle 2D a été réalisé. Le maillage transversal est moins raffiné, cependant, lorsqu’on observe la comparaison des différences des résultats en fonction de la taille des mailles, on ne s’attend pas à des grands écarts.
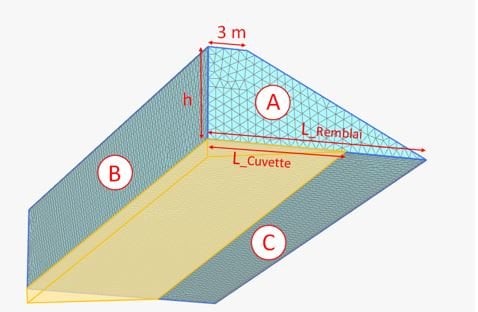
Les conditions limites sont similaires à celles du calcul 2D. Les faces A, B et C de la Figure 6 sont bloquées selon les axes normaux aux plans et sont libres selon les deux autres axes. Trois modèles 3D ont été créés avec les 3 hauteurs : 1, 4 et 7 m.
La longueur de l’affaissement dans la direction longitudinale du remblai est prise égale à 50 m, soit la longueur totale du modèle. Cela correspond à une situation équivalente à l’hypothèse des déformations planes en 2D.
La Figure 7 présente les isovaleurs des déplacements verticaux pour h = 5m. On observe un comportement similaire au modèle 2D. Les déplacements dans la longueur du remblai sont constants. Aucun effet de bord n’est visible. Les valeurs numériques du déplacement sont donc comparées pour une section au milieu du remblai.
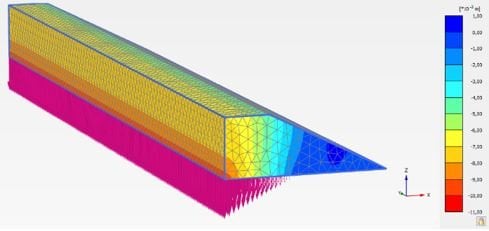
Figure 7. Déplacement selon l’axe z d’un remblai de 5 m avec un déplacement linéaire imposé sur PLAXIS 3D.
Le Tableau 5 compare le tassement différentiel issu du modèle 2D et du modèle 3D pour les 3 hauteurs de remblai.
Tableau 5. Comparaison entre le 3D et le 2D
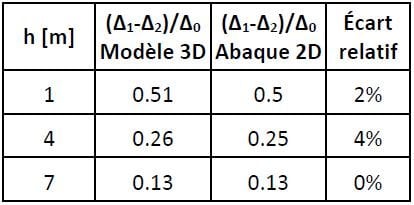
Les valeurs obtenues avec le modèle 3D et celles obtenues avec l’abaque sont très similaires avec des erreurs inférieures à 5% qui peuvent être causées par des lectures imprécises de l’abaque. Ces résultats sont satisfaisants et permettent de confirmer les valeurs présentées dans l’abaque.
4.2 Modèle physique
Une maquette d’une tranche de remblai à une échelle 1/20 a été réalisée (Figure 8 et Figure 9). Un déplacement en pied a ensuite été reproduit pour mesurer le tassement différentiel en surface.

La maquette est réalisée dans une caisse en bois avec un double fond. Le sable est disposé sur une plaque flexible reposant sur un système de planches escamotables (Figure 9). Le sable est compacté pour lui donner des valeurs mécaniques homogènes. Le déplacement est imposé au remblai en enlevant une ou plusieurs planches qui contrôlent la largeur de ce dernier. La plaque flexible se déforme alors sous le poids propre du remblai.
Un modèle numérique 2D a été refait à l’échelle de l’expérience. Les paramètres mécaniques du sol ont été prises comme E = 30 MPa et v=0.3. La cohésion est estimée nulle.
Le Tableau 6 compare les résultats expérimentaux avec le calcul numérique 2D.
Tableau 6. Ecarts relatifs entre les valeurs expérimentales et théoriques
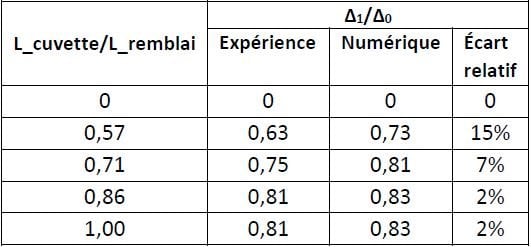
L’expérience ne permet pas d’obtenir des points pour des petites largeurs de déplacement imposées et donne beaucoup d’incertitude pour la valeur de L_cuvette/L_remblai=0,57. Cela peut s’expliquer par la difficulté à lire les différences de niveau inférieures à un demi millimètre. Cependant, les écarts entre les résultats obtenus par les deux méthodes sont considérés comme acceptables, ce qui permet de valider les résultats du modèle numérique réalisé précédemment.
5. EXEMPLES D'APPLICATIONS
Dans le but d’illustrer l’utilisation des abaques obtenus, deux exemples sont proposés.
Dans le premier exemple, on considère un remblai de hauteur h=4m, de largeur 11 m (pente ½) ; le tassement a une largeur transversale de 5,5 m (soit L_cuvette/L_remblai=0.5) et une longueur importante permettant de respecter l’hypothèse des déformations planes, E=30Mpa et ∆0 = 0.01 m.
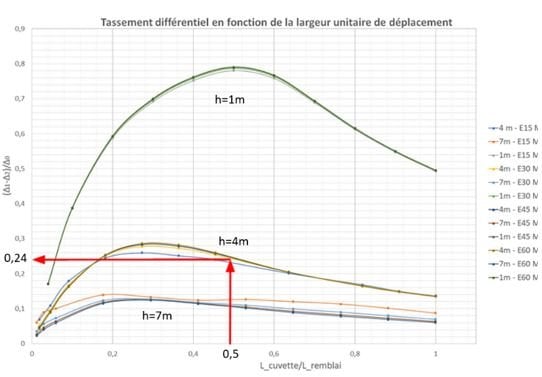
La valeur obtenue pour le taux de transmission est (∆1-∆2)/∆0 = 0,24 (Figure 10). Ainsi ∆1-∆2 = 0,24*∆0 = 0,0024 m = 2,4 mm. Cela signifie qu’à la surface du remblai, on s’attend à obtenir un tassement différentiel transversal ayant une valeur maximale de 0.8mm/m, alors que le tassement différentiel du remblai en pied est de 1.8mm/m. On constate ainsi une atténuation significative (tassement différentiel divisé par plus de 2).
Dans le deuxième exemple, un remblai de hauteur h=5m est considéré, de largeur 13m (pente ½) ; le tassement a une largeur transversale de 6,5m (soit L_cuvette/L_remblai=0,5) et une longueur de même valeur, E=50 Mpa et ∆0 = 0,02 m.
Dans ce cas il a été réalisé une interpolation linéaire entre les courbes h=4m et h=7m (Figure 11) pour définir les valeurs d’un remblai de hauteur h=5m.
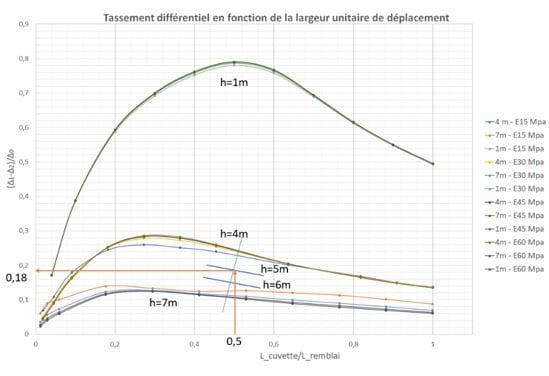
Comme la valeur du module d’Young semble ne pas affecter les résultats, elle ne rentre pas en compte sur la position de la courbe h=5m. La valeur obtenue pour le taux de transmission est (∆1-∆2)/∆0 = 0,18 (Figure 11). Ainsi ∆1-∆2 = 0,18*∆0 = 0,0036 m = 3,6 mm. Cela signifie qu’à la surface du remblai, on constate un tassement différentiel ayant une valeur de 1.2mm/m, alors que le tassement différentiel du remblai en pied est de 3mm/m. On constate ici aussi une atténuation significative (tassement différentiel presque divisé par 3).
6. CONCLUSION
Les résultats obtenus sur ce modèle 2D incitent à une réelle méfiance dès lors que l’on parle de tassement différentiel d’un remblai. Le tassement en pied de remblai diffère significativement de la forme du tassement en haut du remblai. La valeur du tassement différentiel en haut du remblai est d’autant plus atténué (par rapport à la valeur en pied de remblai) que le remblai est haut. Cela peut être affirmé bien qu’il y ait eu un grand nombre de limites dans le développement de cette étude préliminaire (Partie 1 – Elastique linéaire), notamment la considération d’un tassement suffisamment long pour s’affranchir des effets de bord et l’utilisation d’un modèle élastique linéaire, car les différentes méthodes utilisées pour la vérification des résultats permettent de conclure qu’ils sont valides.
Le module d’Young et l’amplitude des déplacements imposés en pied ne semblent pas avoir d’influence significative sur le taux de transmission. Ce point sera vérifié dans la partie II de cette publication (visant à comparer les valeurs avec un modèle élasto-plastique). Des abaques ont été produites afin de synthétiser les résultats et d’avoir un outil opérationnel de prévision simple.
RÉFÉRENCES
Alamaa, A. (2016). High-speed railway embankments— a comparison of different regulations. Stockholm: KTH Royal Institute of Technology .
Bentley Systems. (2019). Reference Manual Plaxis. Edition V20.
Boutonnier, L., Hajouai, F., Bacar Fadhuli , N., & Gandille, D. (2013). LGV EST lot 41 : Tassements calculés puis mesurés sous remblais. Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering. Paris.
GTR . (2000). Réalisation des remblais et des couches de forme. Bagneux: Laboratoire Central des Ponts et Chaussées.
INPL Nancy . (s.d.). Propriétés Mécaniques et Physiques des Sols. Retrieved from http://tice.inpl-nancy.fr/modules/sciences_techniques/Proprietes-Meca-Sols/general/index.html
Larsson, R., Bengtsson, P.-E., & Eriksson, L. (1997). Prediction of settlements of embankments on soft, fine-grained soils. LINKÖPING: SWEDISH GEOTECHNICAL INSTITUTE.
NGUYEN, T., & TRINH, T. (2012). ELEMENTS FINIS : DU CLASSIQUE AU ISOGEOMETRIQUE. Nice: UNIVERSITÉ DE NICE - SOPHIA ANTIPOLIS.
Qin , Y., Zhang, J., Zheng, B., & Ma, X. (2009). Experimental study for the compressible behavior of warm and ice-rich frozen soil under the embankment of Qinghai–Tibet Railroad. Cold Regions Science and Technology, 148-153.
Quezada, J. C. (2014). Mécanismes de tassement du ballast et sa variabilité. Montpellier : Université Montpellier 2.
RFR & SNCF. (2006, Avril 30). IN3279 - Référentiel technique pour la réalisation des LGV - Partie Equipements Ferroviaires. Retrieved from https://victimestgvaccident.files.wordpress.com/2016/12/in3279.pdf
Said-Alami, S., Reiffsteck, P., & Cuira, F. (2017). Méthode d’estimation des tassements des sols fins sous les remblais d’infrastructures ferroviaires pour lignes à grande vitesse. Revue Française de Géotechnique, 153,3.
Techniques de l'ingénieur. (s.d.). Terrassement et géomembranes. Techniques de l'ingénieur.
Terrassiers de France. (2009). Guide pour la réalisation des terrassements des plateformes de bâtiments et d’aires industrielles dans le cas de sols sensibles à l’eau. Paris: Syndicat Professionnel des Terrassiers de France.
Yang, Y., Liu, S., Deng, Y., & Jing , F. (2008). Differential settlement controlling criteria of highway transition sections on soft soil foundation). Dongnan Daxue Xuebao (Ziran Kexue Ban)/Journal of Southeast University (Natural Science Edition).

