Estimation des tassements en partie haute des remblais ferroviaires sur des terrains compressibles (partie 3)

Florent Ménagé, Paula Morales-Garcia, Georges Roederer, Olivier Deck, Rasool Mehdizadeh, Stéphanie Vallerent.

Figure 1.Géométrie et maillage du modèle utilisé pour les calculs.


ABSTRACT
Les deux premières parties de cette publication ont étudié le ratio de transmission du tassement Δ/Δ0 dans une coupe transversale des remblais ferroviaires, avec l’hypothèse des déformations planes (modèles 2D uniquement). Ces modèles permettent d’avoir une première approche de l’estimation des tassements en partie haute des remblais sur des terrains compressibles. Cependant, bien que la géométrie des remblais respecte cette hypothèse dans la plupart des cas, la forme de l’affaissement en pied du remblai ne le fait pas, car elle dépend de divers facteurs tels que l’hétérogénéité du sol support et la distribution des charges imposées. La forme 3D du tassement différentiel en partie basse du remblai pourrait alors être représentée en forme de cuvette transversale et longitudinale. Cette troisième et dernière partie de la publication vise à étudier l’ensemble des paramètres impactant le ratio de transmission du tassement différentiel sur un remblai complet modélisé en 3D.

Cette troisième partie rappelle l’ensemble des paramètres qui influencent le taux de transmission des modèles 2D. On retiendra en particulier que le tassement différentiel au niveau de la sous-couche peut être très différent du tassement différentiel calculé en pied de remblais et que le tassement différentiel longitudinal peut atténuer le tassement différentiel transversal.

Mots-clefs : #Remblais, #Tassements, #ÉlémentsFinis, #Ferroviaire, #Voie, #ConceptionJuste, #SûretéFerroviaire, #Modele2Dvs3D #RaideurSurfaciqueEquivalente

INTRODUCTION
Dans la première partie de cette publication un abaque a été construit, permettant de déterminer le ratio de transmission Δ/Δ0 en fonction de la hauteur du remblai et du déplacement imposé en partie basse. Cependant, les modèles développés ont été faits avec des hypothèses simplificatrices de la loi de comportement du sol et des conditions aux limites. La deuxième partie de cette publication a donc visé à établir l’incidence que ces hypothèses peuvent avoir sur les résultats, en comparant les tassements obtenus dans la partie I avec ceux obtenus avec des modèles ayant une loi du comportement et des conditions aux limites qui représentent mieux la réalité (modélisation élasto-plastique et condition de contact « liée »).

Toutefois, toutes les analyses ont été faites pour déterminer comment le tassement imposé en partie basse d’une coupe transversale du remblai est transmis en partie supérieure, en utilisant l’hypothèse de déformations planes. Cette hypothèse implique la prise en compte d’une géométrie constante dans le sens longitudinale, ce qui ne correspond pas à la réalité sur un grand linéaire. En particulier, le risque de tassement longitudinale est beaucoup plus élevé qu’un tassement transversal car le sol est beaucoup plus hétérogène sur le linéaire complet d’une ligne ferroviaire qu’au sein de la largeur d’un remblai.

La géométrie du remblai peut être prise comme constante longitudinalement, cette forme trapézoïdale étant assez typique dans ce type de structures ferroviaires. En revanche, la forme de la cuvette peut varier plus facilement en raison des hétérogénéités du sol support, ce qui peut générer également des tassements différentiels dans la direction longitudinale. Il convient donc d’étudier le taux de transmission d’un tassement différentiel longitudinal ainsi que la combinaison des deux.

Pour ce faire, on étudiera d’abord la manière dont le tassement différentiel uniquement longitudinal se transmet au niveau de la plateforme, ensuite on analysera la sensibilité du même tassement vis-à-vis de la hauteur du remblai, et enfin une analyse de l’influence d’un tassement couplé longitudinale et transversale.

1 HYPOTHESES DE MODELISATION EN 3D
1.1 Géométrie du modèle et maillage
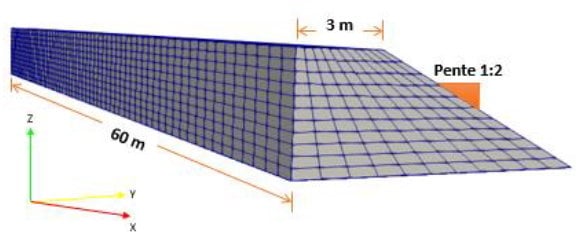
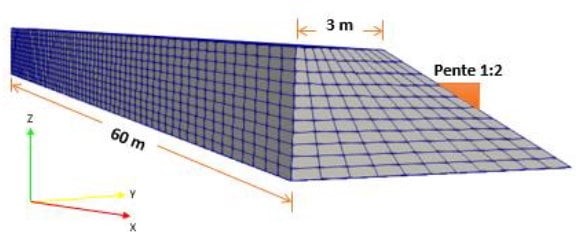
Les modèles réalisés ont été faits sur la moitié droite d’un remblai de section transversale trapézoïdale. La plateforme supérieure du remblai mesure 3 m de large et la pente du remblai est prise de 1/2 (mêmes valeurs que pour les modèles des publications précédents). Afin de ne pas avoir d’effets des bords sur les calculs, un modèle suffisamment long est construit (60m pour une cuvette de 30m de longueur maximum). Les hauteurs de remblais étudiées varient de 2m à 7m ce qui conduit à une largeur de modèle comprise entre 7m et 17m. Le type de maillage 2D choisi est de type « Quadrangle » (hexaèdre une fois extrudé) et la taille maximale des éléments est égale à 1 m (Figure 1).

Figure 1.Géométrie et maillage du modèle utilisé pour les calculs.

1.2 Propriétés géomécaniques
Les calculs sont effectués pour des remblais avec une loi de comportement du sol de type élasto-plastique. Les caractéristiques utilisées sont les suivantes : module de Young de 30 MPa, coefficient de Poisson de 0,3, masse volumique égale à 16 kN/m3, angle de frottement de 30°, cohésion égale à 5 kPa et angle de dilatance de 20° (même valeur que pour les modèles 2D des parties 1 et 2).

1.3 Conditions limites
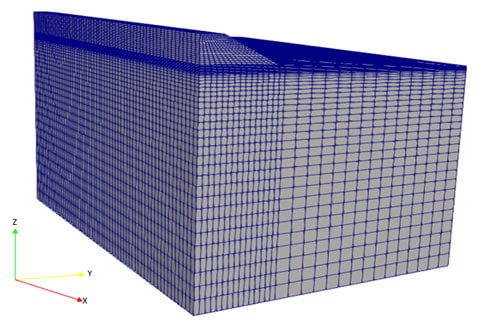
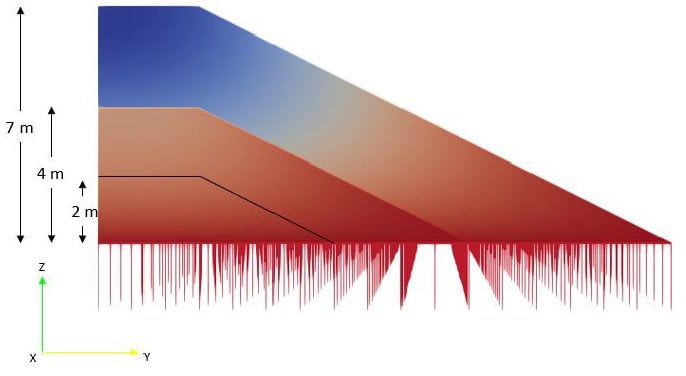
Le modèle 3D n’intègre pas le sol de fondation du remblai. Dans le but de représenter le plus fidèlement possible son influence, les conditions limites sous le remblai sont appliquées au moyen d’éléments de raideur. La même méthodologie de ressorts à raideurs équivalentes déjà adoptée pour la publication Partie II est utilisée pour le modèle 3D. Pour définir la raideur, plusieurs modèles avec un bloc « infiniment » grand sont d’abord réalisés (Figure 2), pour en extraire les raideurs équivalentes. Dans ce cas aussi, la loi de comportement du bloc est définie comme linéaire-élastique, tandis que la loi pour le remblai est élasto-plastique. Un remblai de 4 m de hauteur a été utilisé pour les calculs.

Figure 2. Modèle et maillage du remblai sur un bloc « infiniment » grand de sol

Les résultats montrent que les raideurs verticales (axe Z) et horizontales (axe Y) coïncident avec les valeurs obtenues dans les modèles 2D (Figure 7, publication Partie II). En revanche, les raideurs horizontales suivant l’axe X ne montrent pas de tendance « fiable » permettant de trouver une raideur équivalente. Cette situation est due notamment au fait que les déplacements (<1mm) et réactions sont très petits, ce qui rend très sensible le calcul de raideur (Force/Déplacement). Par conséquent, sur la base de l’hypothèse d’un matériau isotrope, les raideurs de l’axe X sont prises égales à celles de l’axe Y.

On vérifie à l’aide d’un modèle de remblai 3D sur ressorts équivalents (Figure 3), avec des raideurs égales à celles trouvées précédemment (comme itération de départ), que le comportement du remblai est identique. On modélise un remblai sur un sol de fondation caractérisé par un module de Young de 30 MPa ce qui équivaut à une raideur verticale kz = 2MN/m, et des raideurs surfaciques kx = ky = 10MN/m. Les résultats du modèle 2D permettent d’économiser le temps de la recherche itérative de la « bonne raideur ». On réalise directement la « vérification ».

Figure 3. Modèle et maillage du remblai à ressorts

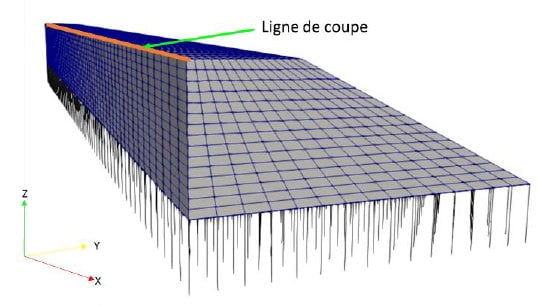
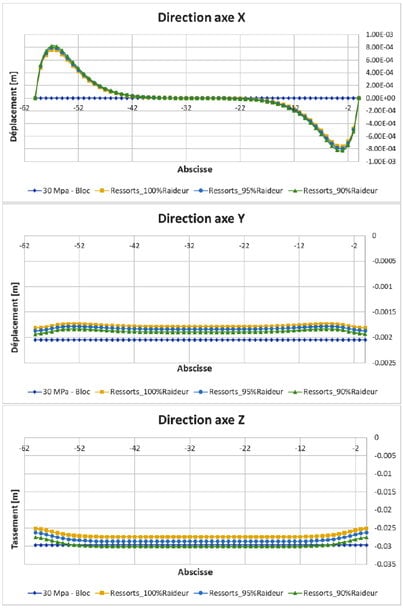
La comparaison est faite sur une ligne de coupe longitudinale (direction x), située en haut du remblais (Z=4m), à l’extrémité de la plateforme (Y=3m ; Figure 3). Il faut d’abord noter que le déplacement en X montre assez bien les effets de bord en raison des conditions aux limites du modèle. Bien que le déplacement soit très petit, un pic est observé dans les premiers mètres des deux côtés du modèle. Malgré cela, les déplacements sont jugés acceptables vers la moitié du modèle (zone où nous appliquerons le tassement différentiel).

Pour les axes Y et Z, l’écart entre les déplacements du modèle équivalent et les déplacements du modèle avec un bloc est modéré (inférieur à 9%). Cette situation est cohérente avec ce qui a été trouvé dans les modèles 2D publié dans la partie 2 où il a été conclu qu’il fallait mettre un coefficient sur la raideur calculée. Des modèles avec une raideur égale à 95% et 90% de la valeur de la raideur calculée sont alors testés. Les déplacements obtenus sont plus proches des résultats obtenus avec le modèle complet qui intègre explicitement un sol de fondation « infiniment épais ». Compte tenu que le déplacement le plus important pour l’étude est le déplacement vertical (suivant l’axe Z), on utilisera uniquement le coefficient de 90% sur les raideurs calculées pour construire le modèle équivalent.

Figure 4. Comparaison des déplacements en haut du remblai (extrémité droite de la plateforme), obtenus avec un modèle global intégrant le sol de fondation et un modèle simplifié avec des ressorts à ses conditions limites.

1.4 Déplacement imposé
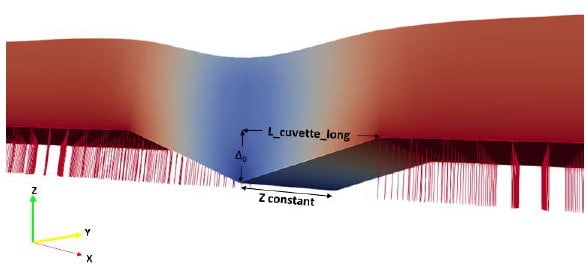
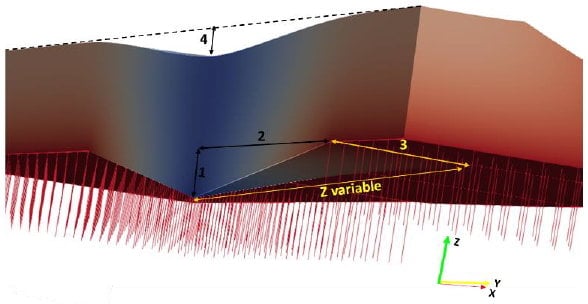
Comme pour les analyses transversales, la cuvette dans la coupe longitudinale a une forme triangulaire. Dans le cas « 3D », elle est centrée sur l’abscisse X=-30 m. Dans le sens transversal elle est soit uniforme, soit également triangulaire. Dans le premier cas, on parlera de cuvette en prismatique (Figure 5). Dans le second cas, on parlera de cuvette pyramidale (Figure 6). La demi-cuvette longitudinale est appelée « L_cuvette_long », et la demi-cuvette transversale « L_cuvette_tran ». Pour une cuvette en V, L_cuvette_tran est égale à la largeur du modèle et il n’y a pas de déplacement différentiel transversal. Le tassement maximal imposé est appelé « Δ0 » et le tassement au niveau de la face supérieur du remblai appelé « Δ1 » (au milieu de la plateforme ferroviaire) et « Δ2 » (tête de remblai) pour le tassement à l’extrémité droite de la plateforme (Figure 6).

Figure 5. Illustration d’une cuvette prismatique.

Figure 6. Illustration d’une cuvette pyramidale. Notation adoptée dans la publication. 1 : « Δ0 », 2 : « L_cuvette_long », 3 : « L_cuvette_tran », 4 : « Δ1 ».

2 ANALYSE DE SENSIBILITE DU TAUX DE TRANSMISSION LONGITUDINAL
Dans ce chapitre, on étudie la sensibilité du tassement différentiel longitudinal en partie supérieure du remblai suivant différents facteurs (longueur de la cuvette, hauteur du remblais, amplitude du tassement, forme du tassement, etc..). Pour cela, on étudie d’abord l’influence d’un tassement imposé uniquement longitudinalement (forme de « V »), puis on fera un lien avec les parties précédentes, en analysant des modèles avec un tassement combiné : transversal et longitudinal.

2.1 Sensibilité à l’amplitude et la longueur du tassement différentiel pour une cuvette prismatique
Il est procédé à une analyse de la sensibilité du taux de transmission du tassement différentiel au sommet du remblai, en fonction de la variation de la taille de la cuvette longitudinale et de l’amplitude du tassement différentiel. À cette fin, on fait varier le tassement différentiel pour différente longueur de cuvette longitudinale. A noter qu’il y a absence de déplacement différentiel transversal (Figure 5). Les tassements différentiels imposés longitudinalement sont de 1mm/m, 2mm/m et 5mm/m pour les « L_cuvette_long » de 2m, 5m, 10m et 15m (soit 12 modélisations). Un remblai de 4 m de hauteur est utilisé pour les calculs et les raideurs surfaciques des ressorts correspondent à un sol de fondation de 30 MPa.

L’analyse est effectuée pour les lignes de coupe situées entre X=0 et X=-60, à la hauteur Z=4 (sommet du remblai), et aux abscisses Y=0, 1m, 2m et 3m (Figure 7).

Figure 7. Lignes de coupe utilisées pour l’analyse du tassement en haut du remblai.

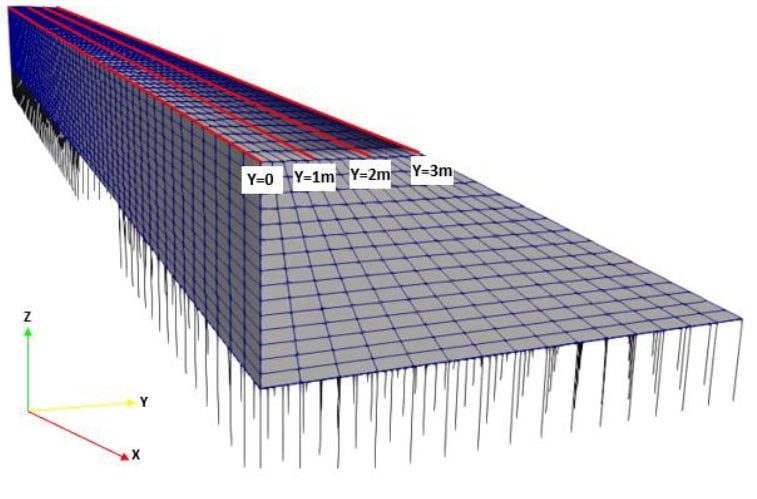
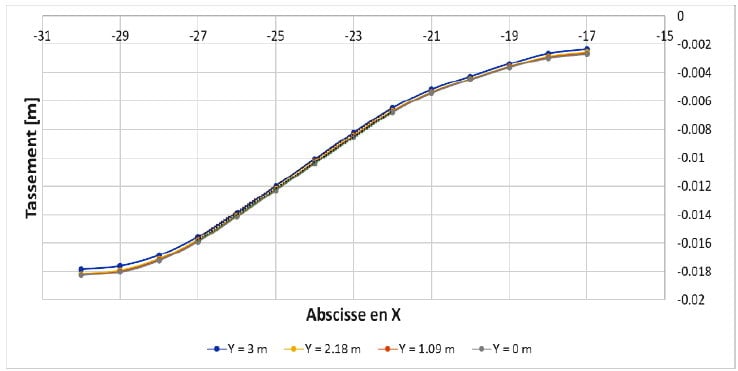
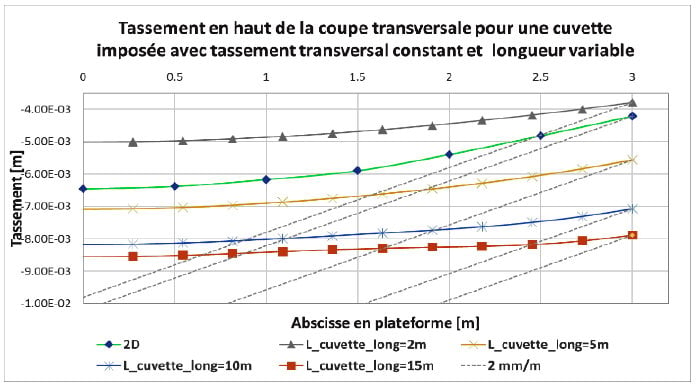
Étant donné l’absence de tassement différentiel transversal, on constate une variation des déplacements verticaux entre les différentes lignes de coupe inférieure à 1%. Il est donc choisi de ne retenir que les valeurs de la ligne Y=0 (Figure 8). Par ailleurs, le tassement différentiel en haut du remblai est défini et calculé comme la pente maximale de la cuvette (Figure 8). Cette définition du tassement différentiel diffère légèrement de celle adoptée dans les parties précédentes (partie I et II). Pour ces études, la variation du tassement transversal était quasi-linéaire. Le tassement différentiel était alors défini comme la différence entre les déplacements au centre et au bord de la plateforme divisée par la largeur de la demi-plateforme. Sur la figure 8 par exemple, on calcule le tassement différentiel à partir du tassement différentiel entre les abscisses X= -27 et X=-23.

Figure 8. Lignes de coupe utilisées pour l’analyse du tassement en haut du remblai. Cas de L_cuvette_long = 10m, Δ0 = 2cm.

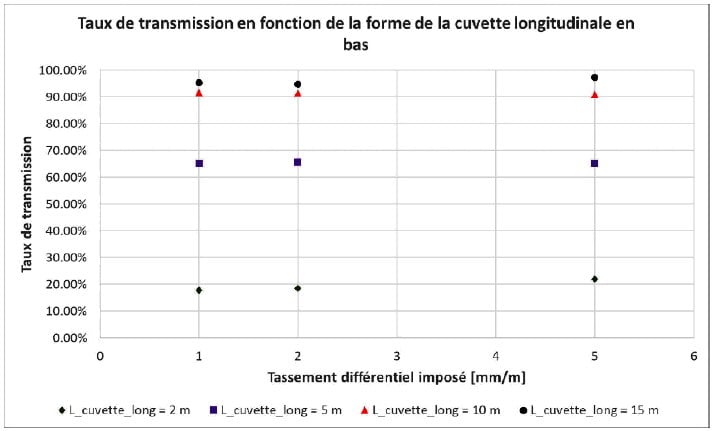
Le taux de transmission est ensuite calculé comme la relation entre le tassement différentiel calculé en haut divisé par le tassement différentiel imposé en bas (Δ0/L_cuvette_long). Les résultats présentés sur la Figure 9 permettent de conclure que le taux de transmission est indépendant de l’amplitude du taux de déflexion imposé. Pour une même longueur de cuvette « L_cuvette_long », les différences sont inférieures à 4%. Cela permet de justifier que le taux de transmission ne dépend pas de l’amplitude du déplacement imposé, mais de la longueur de la cuvette en bas du remblai.

Figure 9. Taux de transmission du tassement différentiel en fonction du tassement différentiel imposé en bas de remblai et de la longueur de la cuvette.

2.2 Sensibilité à la hauteur du remblai pour une cuvette prismatique
Pour évaluer l’impact de la hauteur du remblai, trois modèles de différentes hauteurs ont été réalisés (2m, 4m et 7m) (Figure 10), en maintenant le même taux de tassement différentiel (2mm/m) et les mêmes caractéristiques mécaniques du remblai et des ressorts.

Figure 10. Modèles de différentes hauteurs testées

Comme dans le chapitre 2.1 de cette publication, l’analyse est faite pour la ligne de coupe située au sommet de chaque remblai, aux abscisses Y=0, Y=1m, Y=2m et Y=3m. Cependant, les faibles différences entre les résultats permettent d’analyser seulement une des lignes, Y=0 dans ce cas.

Les tassements obtenus en haut du remblai sont montrés dans la Figure 11. Sur cette figure, on constate en particulier que le tassement différentiel en haut du remblai est atténué à mesure que la hauteur du remblai augmente.

Figure 11. Tassement en haut pour des remblais de différente hauteur et une tassement différentiel imposé en pied remblai de 2mm/m.

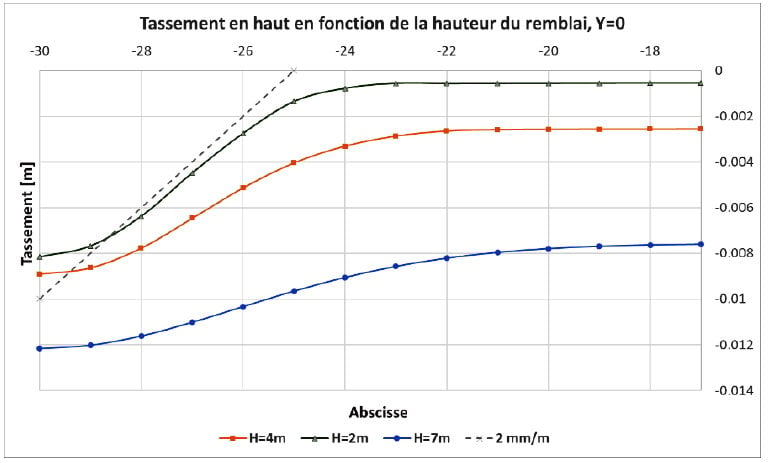
Le taux de déflexion en haut est alors calculé comme la pente de la partie linéaire de la cuvette d’affaissement obtenue en haut (Tableau 1).

Tableau 1. Taux de transmission du tassement différentiel imposé (2mm/m)

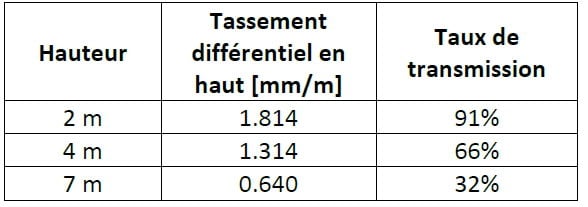
Ces résultats sont cohérents avec les analyses faites dans les parties I et II de cette publication. Plus le remblai est haut et plus ils atténuent le tassement différentiel (tassement longitudinal dans ce cas). Un remblai de faible hauteur atténue très peu le tassement différentiel. On peut donc confondre le tassement différentiel en pied de remblais et en haut du remblai. Cependant, un tassement différentiel sur un remblai de 2m de hauteur semble peu probable. Les tassements différentiels se produisent essentiellement pour des surcharges importantes.

2.3 Sensibilité pour une cuvette pyramidale (lien Partie I et II)
2.3.1 Impact du tassement longitudinal sur le tassement transversal
Afin d’évaluer la manière dont le tassement différentiel longitudinal peut affecter les tassements différentiels transversaux en partie supérieure du remblai, une analyse est effectuée à partir de l’imposition à la fois d’une cuvette longitudinale et une cuvette transversale.

À cette fin, on étudiera d’abord, pour une même cuvette transversale imposée, l’impact de la longueur de la cuvette longitudinale sur le tassement différentiel transversal en haut du remblai. Le modèle évalué est un remblai de 4 m de hauteur sur des ressorts équivalents à un bloc de 30 MPa de portance, avec un tassement différentiel transversal imposé égal à 2mm/m (Δ0=0.01m et « L_cuvette_tran » = 5m). Les longueurs des cuvettes longitudinales évaluées sont « L_cuvette_long » = 2m, 5m, 10m et 15m qui correspondent à des tassements différentiels longitudinaux compris entre 0,66 et 5mm/m. La section transversale analysée se trouve à la moitié du modèle (X=-30m).

Les tassements obtenus au niveau de la plateforme du remblai, dans la coupe transversale, sont montrés dans la Figure 12 et le Tableau 2. Ces valeurs sont comparées aux tassements obtenus précédemment avec un modèle transversal 2D ayant le même remblai, conditions aux limites et déplacement imposé.

Figure 12. Tassement différentiel en haut de la coupe transversale du remblai, pour des différentes longueurs des cuvettes longitudinales

Tout d’abord, il s’ensuit des résultats obtenus que le tassement différentiel obtenu en haut du remblai est atténué par rapport au tassement différentiel imposé en partie basse quel que soit le cas analysé (pente des lignes pointillés vs pente des lignes continues sur la Figure 12 et taux de transmission sur le Tableau 2). Le taux de transmission du tassement différentiel obtenu avec le modèle 2D est supérieur à celui obtenu avec les modèles 3D (Tableau 2).

Tableau 2. Tassement différentiel en haut de la coupe transversale du remblai, pour des différentes longueurs des cuvettes longitudinales

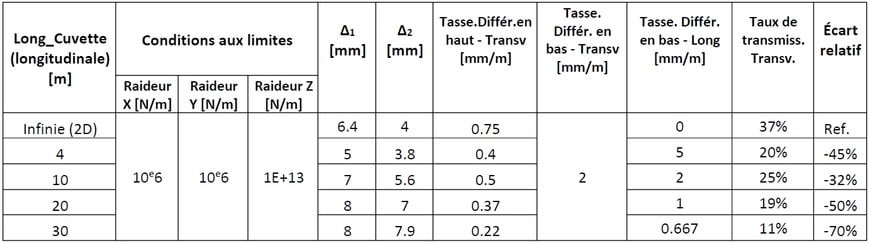
Les écarts relatifs calculés montrent que la prise en compte de la cuvette longitudinale impacte le taux de transmission du tassement différentiel dans la coupe transversale du remblai, le modèle 2D étant (cuvette longitudinale infinie) le plus pénalisant (Tableau 2). Cela s’explique notamment par un transfert d’une partie du tassement différentiel (dans le cas 2D) vers un tassement homogène qui n’est pas ou peu préjudiciable pour la pérennité de la voie ferrée. Cette atténuation pourrait être due au fait qu’en présence d’une cuvette longitudinale, le vide créé par celle-ci absorbe une grande partie du matériau du corps qui équilibre les tassements différentiels. Cependant l’explication de l’atténuation du tassement transversale par tassement longitudinal n’est pas l’objet de cette publication.

2.3.2 Impact du tassement transversal sur le tassement longitudinal
Pour évaluer l’impact d’un tassement différentiel transversal en pied du remblai sur le tassement longitudinal en haut du remblai, le même modèle à ressorts utilisé dans le chapitre 2.3.1 est évalué, mais, dans ce cas, la cuvette longitudinale est fixée à 2mm/m avec Δ0=0.01m, L_cuvette_long=5m, et la cuvette transversale prend les largeurs de L_cuvette_tran=5m, 7m et 10m (tassement différentiel transversal variant entre 0 et 2 mm/m)

Les points analysés se situent sur la ligne située à Y=0, en haut du remblai.

Les cuvettes obtenues en haut du remblai, sens longitudinal, montrent que le tassement différentiel est inférieur au tassement imposé en pied, car les pentes des parties linéaires des cuvettes sont moins fortes que la pente de la ligne représentant le tassement imposé en bas (2mm/m) ( Figure 13). On parle alors d’une atténuation du tassement imposé, qui varie en fonction de la cuvette transversale imposée.

Figure 13. Tassement différentiel en haut du remblai, suivant l’abscisse Y=0, pour des différentes longueurs des cuvettes transversales

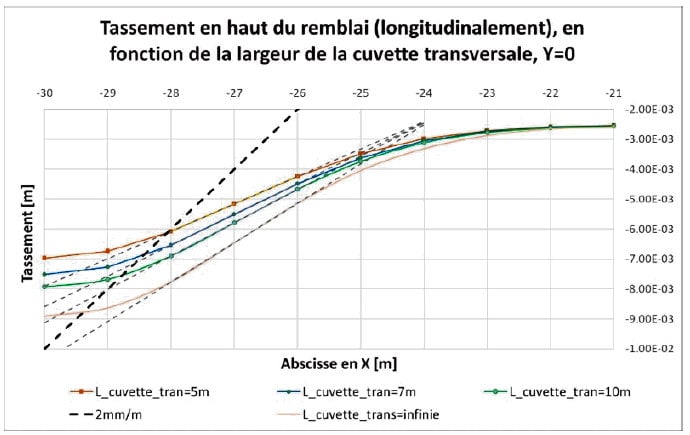
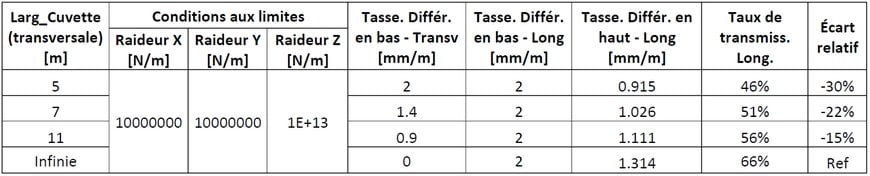
Cette atténuation peut être plus facilement identifiée dans le Tableau 3, où l’on constate que le taux de transmission augmente conformément à l’augmentation de la largeur de la cuvette transversale. Un cas extrême est trouvé lorsque le tassement est imposé seulement longitudinalement, avec un tassement différentiel nulle dans la coupe transversale ; dans ce cas, le taux de transmission qui en résulte est de 66%, qui représente la valeur la plus élevée.

Les écarts relatifs calculés ici (Tableau 3) montrent que la prise en compte de la cuvette transversale réduit le taux de transmission du tassement différentiel dans le sens longitudinal du remblai. Le taux de transmission est d’autant plus faible, que la largeur de la cuvette transversale est également inférieure.

Tableau 3. Tassement différentiel en haut de la coupe longitudinale du remblai, pour des différentes largeurs des cuvettes transversales

3 CONCLUSION
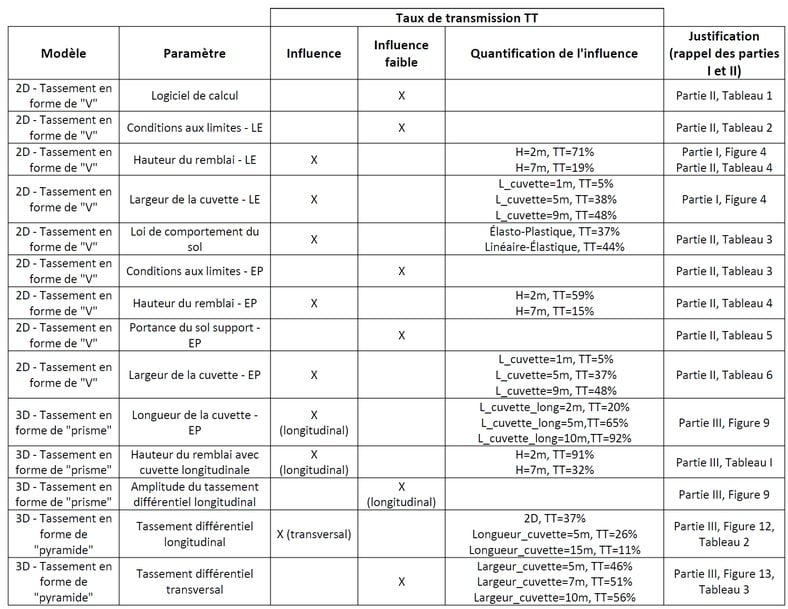
Les modèles et analyses réalisés dans cette troisième partie de la publication permettent de conclure sur l’ensemble des facteurs d’atténuation des tassements différentiels (tableau 4).

Les résultats présentés dans les 3 parties de cette publication permettront aux bureaux d’études ferroviaires de mieux apprécier l’amplitude des taux de transmissions (TT) à considérer en fonction des différentes situations. En particulier, un tassement différentiel longitudinal en pied de remblais de 2mm/m peut être fortement atténué en tête de remblais (0.66mm/m – TT = 32% pour un remblai de 7m de hauteur). Cette connaissance des taux de transmission en fonction des situations permettra ainsi de diminuer les exigences souvent couteuses sur les renforcements de sol pour les remblais de grande hauteur.

Tableau 4. Récapitulatif de l’ensemble des facteurs influençant le taux de transmission des tassements différentiels

REMERCIEMENTS
FMAM remercie les élèves du parcours industrie des Mines Nancy pour leurs apports sur la partie I qui a permis d’amorcer la rédaction des parties II et III.
FMAM tient à remercier en particulier Paula Morales pour sa perspicacité sans faille et son implication au cours de son stage chez FMAM axé sur la publication partie II et III.
Enfin FMAM remercie les enseignants-chercheurs des Mines Nancy et les ingénieurs d’Ingerop qui ont accompagné FMAM tout au long de l’année 2019-2020 dans la rédaction des différentes parties de cette publication scientifique.

REFERENCES
Ménagé, F., Morales-Garcia, P., Roederer, G., Deck, O., Mehdizadeh, R., & Vallerent, S. (2020). Estimation des tassements en partie haute des remblais ferroviaires sur des terrains compressibles (Partie I).
Ménagé, F., Morales-Garcia, P., Roederer, G., Deck, O., Mehdizadeh, R., & Vallerent, S. (2020). Estimation des tassements en partie haute des remblais ferroviaires sur des terrains compressibles (Partie II).

  Demander plus d’information…