lerail.com
04
'20
Written on Modified on
Etude du rayon minimum pour garantir la stabilité des LRS (CWR stability)
Florent Ménagé, Ingénieur voie ferrée chez FMAM
ABSTRACT
Est-ce que Prud’homme et Janin se sont trompés en 1968 sur le comportement des LRS ? Peut-on créer des LRS dans des courbes de rayon R<300m en sécurité ? Cette étude a pour objectif de présenter une modélisation de la voie permettant de passer en revue l’ensemble des facteurs impactant la stabilité des LRS.
L’objectif est double : d’une part, il s’agit de vérifier si nos règles actuelles sont dimensionnées justement, d’autre part de vérifier si des lois simples (linéaires) et pratiques permettent de calculer facilement l’effort transversal lié à une augmentation de température. Pour optimiser la conception et la maintenance des LRS de demain, il est indispensable d’avoir la maitrise des paramètres dimensionnants via des outils accessibles à tous.
Cette publication présente des formules simplifiées de calcul de l’effort transversal de la voie basées sur une modélisation complexe en fonction de différents paramètres (profil de rail, raideur du ballast, amplitude du défaut, rayon de la courbe, etc…) à destination de mainteneurs qui voudraient justifier une demande de dérogation ou faire évoluer son manuel de maintenance des LRS pour des conditions particulières.
Mots-clefs : #LRS, #StabilitéDesLRS, #RayonMinimumLRS, #Tramway, #Ferroviaire, #Voie, #ConceptionJuste
INTRODUCTION
En Janvier 1968, M.A. Prud’homme et M.G. Janin, respectivement Chef de la division des études et recherches « Voie » et chef de la subdivision des Recherches et essais « Voie » ont publié la théorie des LRS décrivant notamment le critère de stabilité sous l’effet des variations de températures. Il s’agit des premières publications (à ma connaissance) indiquant que le rayon minimum d’un LRS est de R300m pour un profil de ballast renforcé et R500 pour profil de ballast normal. Depuis, ces valeurs ont été reprises à l’échelle internationale avec des adaptations.
Dans cette publication historique, on sent les limites liées en particulier au moyen de calcul de l’époque. Tous les calculs sont faits à la main, les résolutions d’équation sont réalisées via des fonctions intermédiaires représentées sous forme d’abaque.
Un peu plus tard, en 1991, Shigeru Miura a publié Lateral track stability: theory and practice in Japan en proposant une approche par le calcul de l’énergie puis en 2003, Nam-Hyoung Lim publie Stability of continuous welded rail track en proposant différentes modélisations éléments finis.
En Juillet 2006, l’université de Chalmers (Suède) publie un article intitulé « A numerical study of the lateral ballast resistance in railway tracks” qui aspire aux mêmes objectifs que les protagonistes précédents :
- Quels sont les paramètres qui comptent vraiment dans le calcul de l’effort transversal des traverses sur le ballast ?
- Y a-t-il des mesures inefficaces malgré tout mise en œuvre sur un réseau ferrée ?
- A quel point sommes-nous sécuritaires en écoutant la théorie de Prud’homme et Janin ?
L’étude la plus récente a été initiée par l’UIC. Elle est intitulée Track stability and prevention of buckling (non-publiée à date).
Toutes ces publications sont souvent complexes car elles étudient la stabilité de la voie ballast mais aussi le domaine plastique de la voie ferrée avec des calculs de déplacements transversaux de la voie ballast de l’ordre du mètre.
La théorie des LRS n’étant plus forcément dans tous les esprits, ci-dessous est un bref rappel des points importants affirmés par Prud’homme et Janin en 1968 :
- La stabilité des LRS est uniquement analysée pour le scénario « Voie à vide » considéré comme le cas le plus pénalisant
- L’effort linéique d’un rail qui se dilate longitudinalement dans une courbe « parfaite » de rayon R est défini comme étant le rapport fcourbe = Fdilatation / R avec Fdilatation = ESαΔT
- Un défaut de soudure mesuré suivant l’angle entre les 2 rails augmente l’effort transversal de la voie sur le ballast suivant la formule fdéfaut soudure = 0.955 β k (avec β l’angle dans le plan horizontal entre les 2 rails soudés et k la résistance élastique de la traverse dans le ballast par ml de voie)
- L’amplitude critique d’un défaut de dressage augmente linéairement en fonction rayon R pour un effort transversal fixé
- Le couple d’encastrement du rail dans la traverse permet de réduire l’effort transversal sur le ballast
- La résistance transversale du ballast est diminuée d’environ 8kN/ml si on considère l’effet des vibrations, un défaut de soudure et un défaut de nivellement (générant un effort vertical vers le haut)
- Le rayon minimum pour un LRS est R300m
L’objectif est de vérifier l'ensemble de ces constats et affirmations déjà démontrés mais cette fois-ci via une modélisation en éléments finis qui permet la réalisation de géométries quelconques.
Il conviendra d’être vigilent sur les valeurs utilisées par Prud’homme et Janin qui compte toujours en rail + demi-traverse (en effort et en résistance) alors que les valeurs dans la littérature ferroviaire comptent 2 rails avec une traverse complète. On retiendra que la résistance transversale d’une demi-voie ballast stabilisée avec « traverses mixtes » est de 5.9kN/ml (une demi-traverse et 1 rails selon la publication de Prud’homme et Janin), soit 11.8kN/ml de voie complète et de 15kN/ml pour 1 traverse et 2 rails selon le livre Track Compendium de Bernhard LICHTBERGER. Il s’agit là de valeurs de « pic » de résistance.
LE CAS DE CHARGE « VOIE A VIDE », EST-IL LE CAS LE PLUS PENALISANT POUR LA STABILITE DU LRS?
Conformément aux valeurs de la fiche UIC774-3, la résistance longitudinale de la voie non-chargée bien entretenue est de 20kN/ml et de 60kN/ml lorsque la voie est chargée (sous-entendu à 23tonnes/essieu). Le chargement du matériel roulant apporte donc une « sur-résistance » de +40kN/ml.
Conformément à la fiche UIC518, l’effort transversal maximal que le matériel roulant peut exercer sur une voie est de 42.5kN/ml. Il s’agit d’un maximum qui est rarement atteint car il faut que l’effort réellement exercé par le matériel roulant soit inférieur pour être homologué. Les constructeurs visent donc généralement une valeur de 80% de cette limite pour garantir l’essai d’homologation. Fort de cette constatation où l’effort transversal exercé par le matériel roulant est globalement inférieur ou égal à la résistance supplémentaire apportée par le poids du matériel roulant, il est donc pertinent de se focaliser sur le cas de charge « Voie à vide » comme l’a fait Prud’homme et Janin dans leur étude.
EST-CE QUE LA FORMULE « FLATERAL = FDILATATION LONG / R AVEC FDILATATION = ESΑΔT » EST VRAIE ? APPROCHEE ?
Dans la grande majorité des notes de calcul visant à démontrer la stabilité de la voie, on trouve une formule, généralement non-démontrée, qui relie l’effort transversal à l’effort de dilatation longitudinal et au rayon de la courbe :
ftransversal linéique = Fdilatation longitudinal / R avec Fdilatation = ESαΔT.
La démonstration qualitative s’apprécie par une annulation de proche en proche des forces de dilatation longitudinales tant que les tranches élémentaires de rail sont colinéaires (en appliquant un bilan des efforts sur des tranches de rails et le principe mécanique d’action/réaction). Dès lors que la colinéarité n’est plus vérifiée, on constate implicitement un reliquat de l’effort longitudinal. Ce reliquat d’effort longitudinal est issu de la résultante non-nul des efforts longitudinaux pour une tranche de rail. Cette résultante est identique sur l’ensemble de la courbe pour un rayon R constant.
Dans la théorie de Prud’homme et Janin, on lit que l’effort transversal en courbe est composé d’un terme en F/R (notre fameuse formule) et d’un terme en Acos(ωx) correspondant à un défaut de géométrie dressage dans la courbe. Dans le cas d’une courbe parfaite, Prud’homme et Janin affirment que l’effort linéique transversal est ftransversal linéique = Fdilatation longitudinal / R avec Fdilatation = ESαΔT. Le terme en Acos(ωx) dépend en particulier de Iyy’ (moment quadratique du rail suivant l’axe yy’) et la raideur rotative de l’attache K exprimé en kN/rad. Dans cette publication on retiendra la valeur de K comme étant égale à 100kN/rad.
Afin de vérifier la formule pour la courbe dite « parfaite », c’est-à-dire sans défaut de géométrie, on a modélisé sur un logiciel éléments finis (Code_Aster) : un rail 50E6 (modélisé comme une poutre d’Euler) reposant sur des ressorts de raideur : kx (pour rail + ½ traverse) = 5kN/mm, ky=1.56kN/mm (2.6x106 N/m/ml pour des traverses bétons stabilisées avec un profil de ballast normal ou renforcé) et kz = 100kN/mm, krx = 1N/rad (raideur impactant la torsion du rail), kry = 1N/rad (impactant la flexion verticale) et krz = 100kN/rad (impactant la flexion transversale). Les ressorts sont espacés de 60cm dans cet exemple :
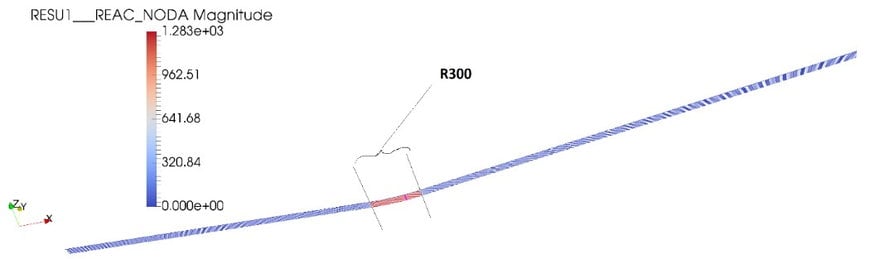
L’effort transversal perpendiculaire au rail en pleine courbe est de 2,065kN/ml (valeur moyenne de 2,061kN/ml et valeur de pic en début et fin de courbe à 2,138kN/ml) alors que le calcul via la formule f= F/R donne un résultat de 2,073kN/ml, soit un écart de 0.6% sur la valeur moyenne et un écart de 0.4% sur la valeur de pic. L’erreur relative est insignifiante par rapport à notre connaissance des valeurs de résistance du ballast. On peut donc conclure que pour une courbe parfaite (sans défaut de géométrie), la formule f=F/R avec F l’effort de dilatation longitudinal du rail donne un résultat satisfaisant pour l’utilisation que l’on en a.
On constate aussi que les valeurs krx, kry et krz n’ont aucune influence sur le résultat.
EST-CE QUE LA FORMULE « FDEFAUT SOUD = 0.955*Β* K » EST VRAIE ? QUELLE EST SON IMPACT PAR RAPPORT A NOS TOLERANCES DE SOUDURE ACTUELLES ?
Les tolérances de soudures usuellement imposées dans les marchés sont de +/-0.5mm dans le plan horizontale et verticale, mesurées sur une règle de 1m. Il serait cependant possible d’utiliser la catégorie W et X de la norme EN14730-2 qui interdit des flèches de rail « rentrante ». Cela permet d’avoir au maximum 1 soudure de rail qui encourage le flambement du rail. Les tolérances de soudure de la norme « soudure » aurait-elle été rédigé pour limiter les risques d’instabilité de la voie ballast ?
Par la manière de calculer l’effet d’un défaut de soudure, l’étude de Prud’homme et Janin considère que le rail extérieur courbe à un défaut avec une flèche sortante et le rail intérieur courbe à un défaut avec flèche rentrante.
Le même modèle éléments finis utilisé est le même que celui utilisé précédemment. Nous obtenons les résultats suivants pour différentes valeurs de tolérance de soudure et profilé de rail :
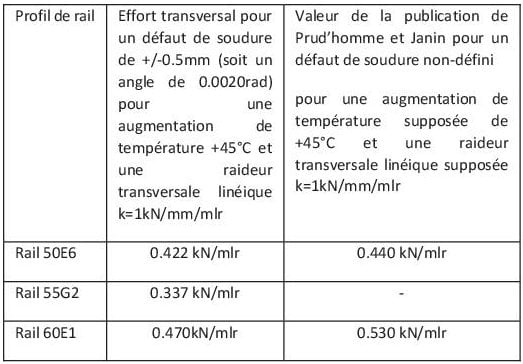
Les valeurs trouvées sont comparables étant donné les incertitudes sur le défaut de géométrie considéré et la raideur transversale linéique choisie par Prud’homme et Janin pour leur étude.
Le choix du profil de rail (entre 50E6 et 60E1 sur le réseau ferré national) impacte peu l’effort transversal linéique au niveau d’un défaut de géométrie. Le sur-effort transversal augmente de +1% (+0.05kN/mlr si on choisit le profil de rail UIC60 au détriment du profil 50E6) de la valeur de la résistance transversale totale du ballast en fonction du choix du profil de rail. Le choix d’un profil de rail 50E6 au lieu d’un profil de rail 60E1 n’a donc pas d’effet significatif sur l’effort transversal en lien avec un défaut de soudure.
De même, la linéarité du paramètre k par rapport à l’effort transversal a été étudié :
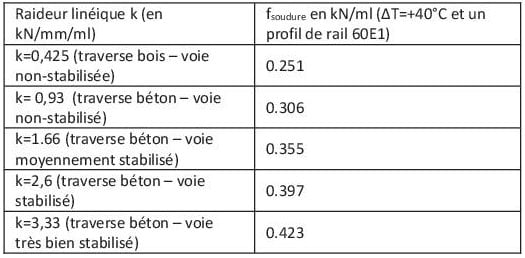
En complétant de quelques valeurs extrêmes réalistes pour le profil de rail 60E1, on trouve la tendance linéaire suivante :
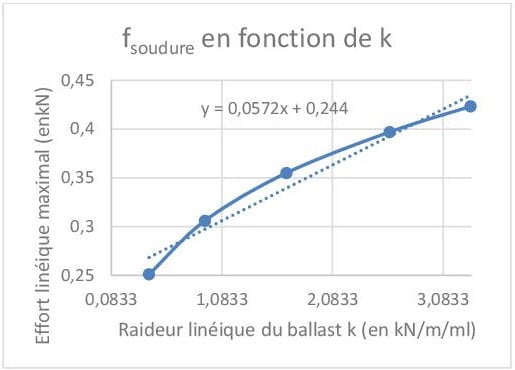
On en déduit que f (k) = 0.057 * k + 0.244. Il y a donc un lien de linéarité entre l’effort transversal linéique et la raideur transversale de la voie sur la plage de valeur usuelle en voie ballast.
La conclusion du graphique ci-dessus peut surprendre le lecteur qui interprète trop rapidement les valeurs présentées. Avec une lecture rapide, on peut croire que : « Plus la voie est consolidée (k élevé), plus l’impact d’un défaut de soudure est pénalisant et plus le risque d’instabilité de voie est élevé ». En fait, plus la raideur transversale de la voie est élevée, plus l’effort transversal au droit de la soudure est élevé mais la marge de sécurité vis-à-vis d’une instabilité reste plus grande pour une voie stabilisée :
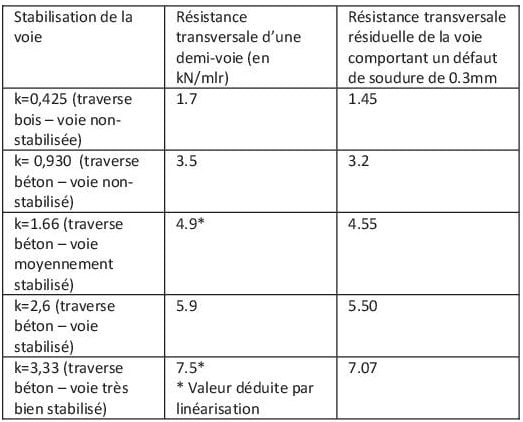
Même si l’impact d’un défaut de soudure est plus impactant sur une voie ayant été stabilisée, la résistance transversale résiduelle reste bien supérieure.
Prud’homme et Janin affirme qu’il y a une relation linéaire entre l’effort transversal et l’angle formé par les rails au niveau du défaut de soudure. Les défauts de rails considérés sont 0.2mm, 0.3mm, 0.4mm et 0.5mm. Ces valeurs sont réalistes et conforme aux valeurs normatives.
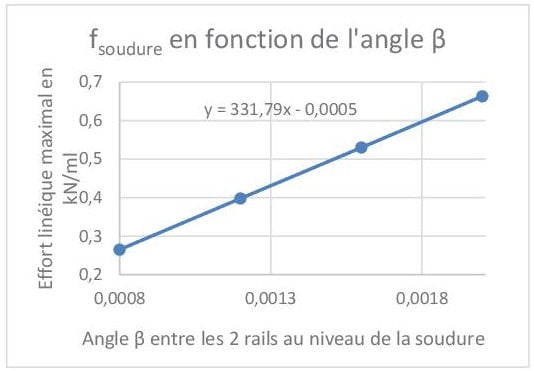
On en déduit que f(β) = 332 x β avec f en kN/ml. Il y a donc bien une linéarité entre l’effort transversal linéique et l’angle formé par le rail dans la plage de tolérance usuelle des soudures de rail.
En revanche, on ne retrouve pas la loi géométrique de Prud’homme et Janin où f(k, β) = A x k x β. Cela signifie que la relation, affirmée et démontrée dans l’étude de Prud’homme et Janin, correspond à un cas particulier ou des hypothèses spécifiques permettant une résolution formelle des équations.
Indépendamment de l’étude de Prud’homme et Janin, il convient de retenir que pour le défaut de soudure maximal (0.5mm) sur les 2 rails (soudure en vis-à-vis), l’un avec une flèche sortante et l’autre avec une flèche rentrante, l’effort transversal généré par ce seul défaut est de 1.4kN/ml alors que la voie peut résister à environ 12kN/ml (valeur de Prud’homme et Janin) à 15kN/ml (valeur du Track Compedium). On peut donc conclure que dans la pire des situations, le défaut de soudure consomme au 10% maximum de la résistance transversale totale.
Cette conclusion est cohérente avec l’approche de Prud’homme et Janin qui soustrayaient 10% de la résistance transversale totale. Nous proposons donc de retenir uniquement cette conclusion à propos de l’étude de l’impact d’un défaut géométrique de soudure étant donné que la tolérance sur les soudures varie peu d’un projet/réseau à l’autre, de même que la raideur linéique transversale du ballast.
EXISTE-T-IL UN LIEN SIMPLE (LINEAIRE) ENTRE LE DEFAUT DE DRESSAGE MAXIMUM ET LE RAYON DE COURBE R ?
Un défaut de dressage au sens de Prud’homme et Janin est défini comme suit :
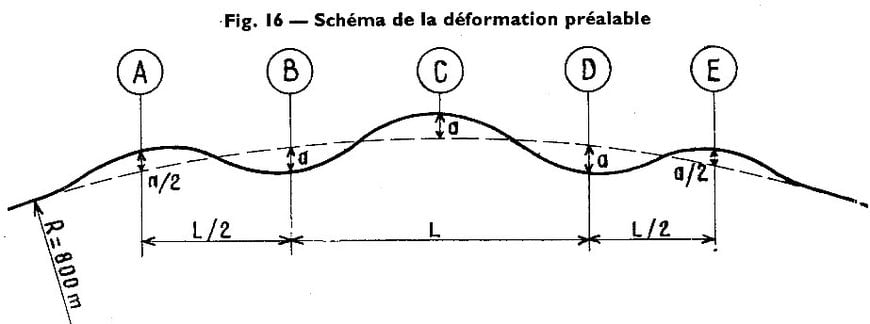
La longueur « Lcritique » a été calculé formellement par Prud’homme et Janin. Cependant, il semble plus pertinent de choisir L en fonction des outils de mesure du quotidien, à savoir la corde de 10m ou le Mauzin (qui mesure la flèche sur une corde de 10m).
Dans la publication Lateral track stability : Theory and practice in Japan de Shigeru Miura, il est fait état de 4 modes de déformation :
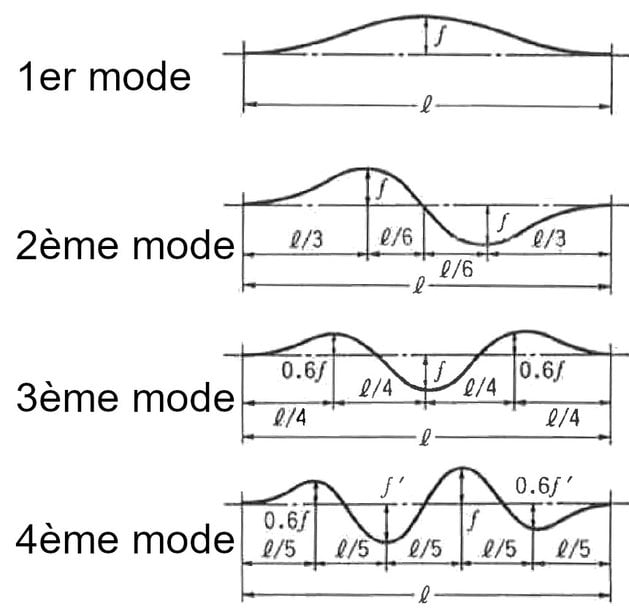
Shigeru Miura conclut quantitativement (en considérant l’énergie liée à la déformation) que, parmi ces 4 modes de déformation, pour des rayons R<700m, l’effort transversal nécessaire pour le 1er mode d’instabilité est inférieur à l’effort transversal nécessaire pour engendrer le 2ème mode d’instabilité. Indépendamment de la démarche calculatoire ayant amenée cette conclusion, le résultat est intuitivement cohérent.
Dans notre étude, nous allons modéliser des défauts de flèche d’amplitude « f » présent sur une longueur de 10m (longueur caractéristique des outils de surveillance de voie) avec une forme de type « 1er mode d’instabilité » qui est le cas le plus probable et qui nécessite l’effort transversal le plus faible pour se produire.
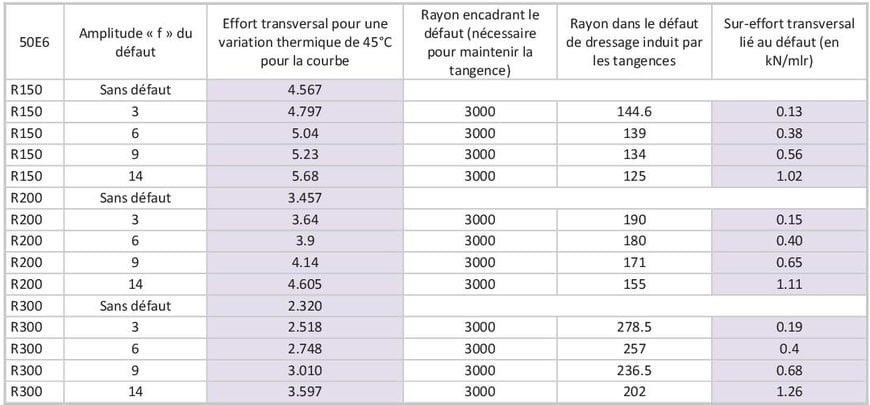
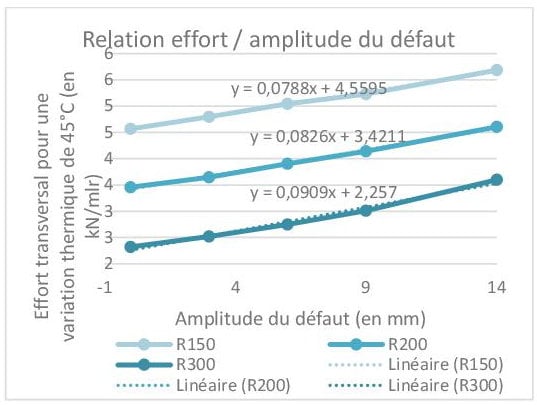
On constate en particulier que sur la plage des défauts de dressage usuels en voie ballast (0 à 14mm sur une distance de 10m), l’effort augmente linéairement avec l’amplitude du défaut et s’ajoute à l’effort transversal d’une courbe parfaite (sans défaut de géométrie) ce qui diffèrent de l’étude de Prud’homme et Janin qui ont affirmé la linéarité entre l’amplitude du défaut et le rayon R pour un effort fixé. Grâce à la relation de linéarité établie entre le rayon, l’amplitude du défaut et l’effort transversal, il est possible d’établir la courbe reliant l’amplitude du défaut au rayon pour un effort transversal fixé :
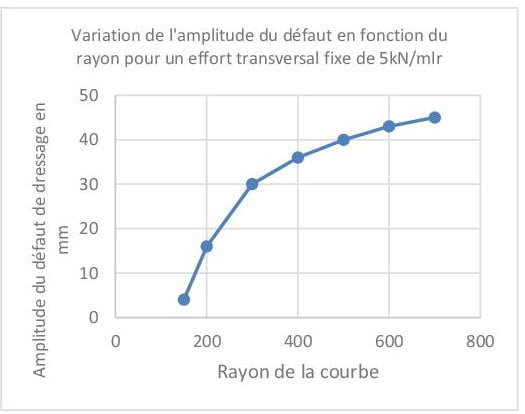
On constate de manière assez prévisible que l’évolution suit une courbe en « – 1/R » (pour être précis, la tendance est en -1/(0.09*R)).
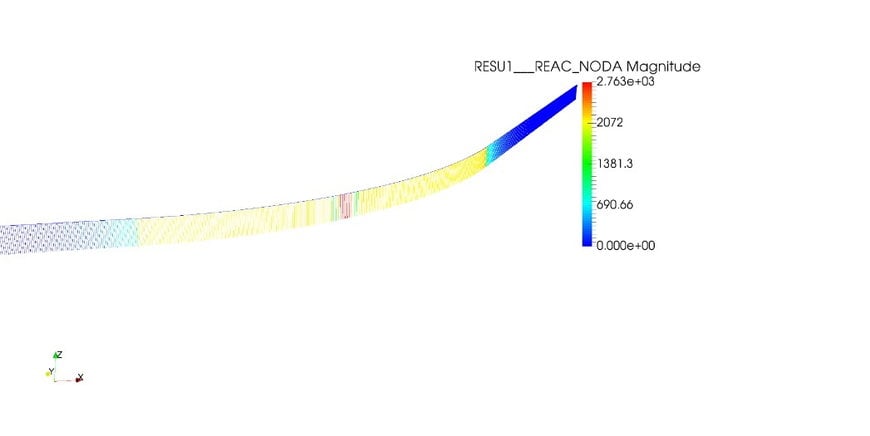
Il a aussi été analysé l’impact d’un défaut dans la courbe de type « Rectiligne » :
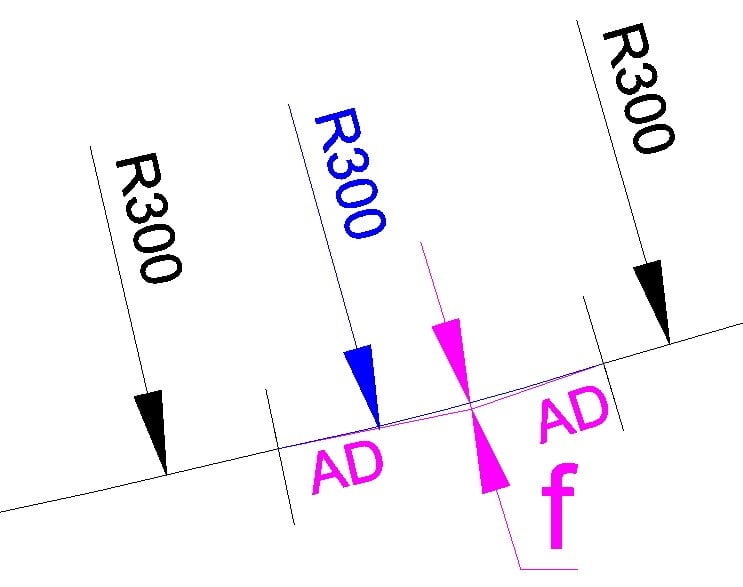
La géométrie du rail testée est donc une courbe R300, puis un alignement droit de 5m tangent à la courbe R300 connecté à un autre alignement droit lui-même tangent au rayon R300. Le défaut créé correspond à la distance entre le sommet de tangence des 2 alignements droit et la courbe R300 initiale (sans défaut).
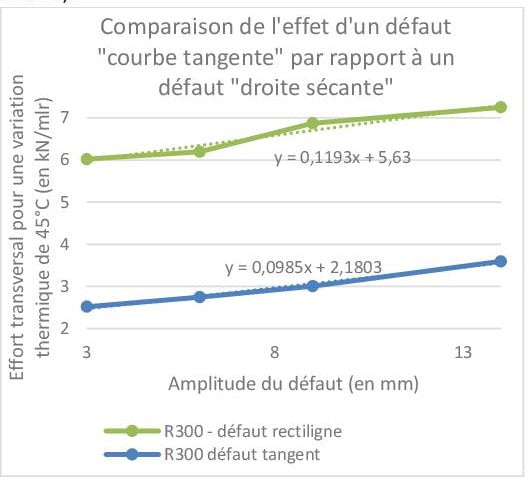
De même, on observe une tendance linéaire entre l’effort induit par le défaut et l’amplitude du défaut pour une plage de défaut choisit conformément avec les tolérances usuelles d’entretien de la géométrie de la voie ballast.
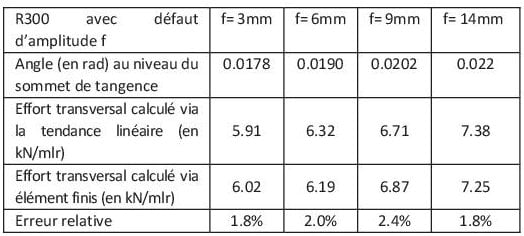
L’effort engendré par un défaut rectiligne dans une courbe est indépendant du rayon de la courbe, il dépend uniquement de l’amplitude du défaut (sous réserve de respecter les hypothèses de calcul, notamment linéaire de 10m et amplitude de défaut inférieur à 14mm). En effet, on retrouve les valeurs d’effort transversal engendré par un défaut rectiligne dans le courbe R300 par application de la tendance linéaire calculée pour un défaut de soudure.
L’angle formé par les 2 alignements droits de 5m tangent à la courbe R300 a été mesuré. Nous avons les valeurs suivantes :
EST-CE QUE LE COUPLE D’ENCASTREMENT DU RAIL DANS LA TRAVERSE INFLUE SUR LES RESULTATS ?
Dans l’étude Prud’homme et Janin, il fait état de l’impact du couple d’encastrement du rail dans la traverse. En particulier, il est affirmé que l’utilisation de selles sur les traverses bois augmente le couple d’encastrement et permet de diminuer le rayon minimum en LRS.
Il y a une incertitude sur la raideur de l’encastrement. La publication Stability of continuous welded rail track de Nam-Hyoung Lim indique une valeur de 166.3 kN.m/rad. La publication de Prud’homme et Janin donne une valeur comprise 166kN/rad (100kN/rad par traverse avec attache RN sans selle) et 250kN/rad (150kN/rad par traverse avec attache RN sans selle).
Avec le modèle aux éléments finis établi (poutre d’Euler sur des ressorts), il n’y a aucune différence notable sur les valeurs de l’effort transversal avec ou sans raideur d’encastrement. Dans le modèle avec raideur d’encastrement, de même, en prenant une raideur d’encastrement 1000 fois plus faible, les résultats restent inchangés. Il est possible que cette absence de sensibilité soit dû à l’opérande du logiciel qui n’agit pas sur les éléments de type « poutre ». Dans la publication de Prud’homme et Janin, d’une part, l’impact du couple d’encastrement intervient en fixant l’hypothèse d’une très faible rotation. D’autre part, ces 2 publications n’explicitent pas l’impact d’une raideur d’encastrement nulle (lié à du jeu dans l’attache). Il s’agit du seul paramètre sur lequel cette publication ne tire pas de conclusion ferme.
EST-CE QU’UN DEFAUT DE NIVELLEMENT EST PREJUDICIABLE ?
Un défaut de soudure de 0.5mm en pointe a été modélisé dans le plan vertical. Pour une augmentation de température de +45°C, l’effort de flambement est de 266N/ml. Plusieurs valeurs de défaut ont été testés. Etant donné la raideur du rail plus élevé dans la direction verticale, la loi de comportement est légèrement différente : f(β) = 220 x β avec f en kN/ml avec β (en rad) l’angle formé par les 2 morceaux de rail de part et d’autre de la soudure mesuré sur une règle de 1m.
Cela signifie en particulier que l’effort de flambement lié à un défaut de soudure dans le plan vertical (coude de soudure) ayant une amplitude f est équivalent à 60%-66% de l’effort de flambement lié à un défaut de soudure dans le plan horizontal (coude de soudure) avec la même amplitude f.
Un défaut de nivellement de la même amplitude que le défaut de dressage a été testé sur la courbe R300. L’effort vertical de soulèvement (lié à un défaut de nivellement « tangent ») est du même ordre grandeur que l’effort transversal (lié à un défaut de nivellement « tangent »). On ne retrouve pas la diminution de 60% que nous constatons sur un défaut de soudure.
Comme les tolérances de maintenance en nivellement autorisent des défauts de nivellement comparable à celle des défauts de dressage, il est donc possible d’avoir un effort vertical supérieur au poids du chassis de la voie. Cela signifie 2 choses :
- Le scénario « Absence de frottement entre la sous face de la traverse et le ballast » est possible
- Un défaut de nivellement peut favoriser l’apparition d’un défaut de dressage par diminution substantielle de la résistance transversale totale (résistance transversale divisée par 2 au droit du défaut de nivellement).
Pour comprendre l’impact du défaut de nivellement sur la résistance transversale, prenons l’exemple d’un défaut de nivellement donc le poids apparent du rail et de la demi-traverse d’environ 10%. On considère que loi de frottement entre la traverse et le ballast est de type « Coulomb ». Il y a ainsi une linéarité entre la diminution d’effort transversal et la diminution d’effort vertical. C’est-à-dire qu’une perte de poids de 10% engendre une diminution du frottement de 10%.
Conformément à différentes publications, on considère que le frottement ballast/traverse représente au maximum 50% de la résistance transversale totale.
On peut ainsi conclure qu’une diminution de la résistance liée au frottement de 10% engendre une perte de résistance transversale totale de 5% (10% * 50%).
QUELLE EST LE RAYON LIMITE EN VOIE LRS ?
Le bilan des efforts transversaux est comme suit (pour un rail 50E6 à +45°C avec k= 2.6kN/mm/mlr) :
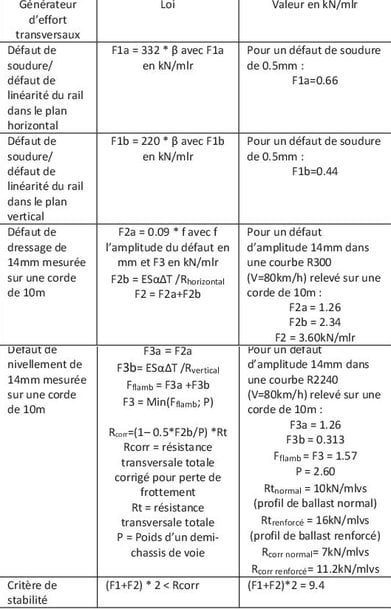
Tous les ouvrages et publications antérieurs ne sont pas unanimes sur la valeur de la résistance transversale de la traverse dans le ballast, ajouté à la question d’utiliser une valeur mesurée ou une valeur de calcul.
Avec les valeurs que nous avons considérées, nous retrouvons le rayon minimum à R=300m avec un profil de ballast renforcé et un rayon minimum R=500m avec un profil de ballast plein (ou normal) ce qui est cohérent avec les règles de maintenance en vigueur sur le réseau ferré national.
CONCLUSION
Cette étude démontre qu’il est possible avec des paramètres simples de calculer l’effort transversal exercé par les traverses sur le ballast en cas d’augmentation de température. Les valeurs obtenues sont conformes aux valeurs appliquées depuis des années ce qui est rassurant vis-à-vis des règles de maintenance et confirme que l’approche simplifiée présentée dans cette étude est viable.
La théorie de Prud’homme et Janin est impressionnante et vraisemblablement atemporelle. 50 ans plus tard avec des outils de calcul beaucoup plus puissant, nous arrivons aux mêmes conclusions avec de petites nuances qui n’ont pas d’importance.
Cette étude permettra en particulier à un décideur de mesurer le paramètre d’intérêt : Puis-je réaliser un LRS dans une courbe de rayon R<300m si mes conditions climatiques révèlent qu’une augmentation de température de +45°C est improbable ? Puis-je autoriser un défaut de géométrie plus important si je choisis une traverse plus lourde ? etc… Avec ces relations simplifiées, il est possible d’adapter sa conception et sa maintenance en choisissant sciemment le compromis que l’on fait et le risque que l’on prend.
Auteur :
Florent Ménagé, Ingénieur voie ferrée chez FMAM
Email : This email address is being protected from spambots. You need JavaScript enabled to view it.
References :
1. E Kabo - A numerical study of the lateral ballast resistance in railway tracks – 2006
2. Bernhard Lichtberger – Track Compendium – 2005
3. Nam-Hyoung Lim, Nam-Hoi Park, Young-Jong Kang – Stability of continuous welded rail track – 2003
4. Coenraad Esveld - Improved knowledge of CWR track - 1992
5. Gopal Samavedam, Andrew Sluz, Andrew Kish - the effect of realignment on track lateral stability – 1999
6. Shigeru Miura - Lateral Track Stability: Theory and Practice in Japan – 1991
7. M.A. Prud’homme, M.G. Janin – La stabilité des voies en long rails rails soudés – 1968

